题目内容
(本小题满分13分)某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若
企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分
别为 万元(m >
0且为常数).已知该企业投放总价值为10万元的A、B
万元(m >
0且为常数).已知该企业投放总价值为10万元的A、B
两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(Ⅰ)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(Ⅱ)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
【答案】
解:(I)设投放B型电视机的金额的x万元,则投放A型电视机的金额为(10 – x )万元,农
民得到的总补贴  4分(没有指明x范围的扣1
4分(没有指明x范围的扣1
分)
(II) ,令y′= 0 得 x=10m –1 6分
,令y′= 0 得 x=10m –1 6分
1°若 10m –
1 ≤ 1 即 0 < m ≤  时 ,则f(x)在为减函数,当x = 1时,f(x)有
时 ,则f(x)在为减函数,当x = 1时,f(x)有
最大值;
2°若 1 < 10m –
1 < 9 即 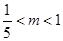 时,则f(x)在
时,则f(x)在 是增函数,在
是增函数,在
 是减函数,当x
= 10m–1时,f(x)有最大值;
是减函数,当x
= 10m–1时,f(x)有最大值;
3°若10m–1≥9 即m≥1时,则f (x)在是增函数,当x = 9时,f(x)有最大值. 10分
因此,当0<m≤ 时,投放B型电视机1万元;当
时,投放B型电视机1万元;当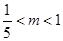 时,投放B型电视机(10m–1)
时,投放B型电视机(10m–1)
万元,当m≥1时,投放B型电视机9万元.农民得到的总补贴最大。13分
【解析】略

练习册系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和