Question

【题目】已知中心在坐标原点，焦点在轴上的椭圆过点，且它的离心率

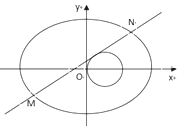
（I）求椭圆的标准方程；

（II）与圆相切的直线交椭圆于、两点，若椭圆上一点满足，求实数的取值范围

Answer 1

【答案】（1）；（2）

【解析】

（1）根据题意先设出椭圆的标准方程，然后根据椭圆上的点及离心率可求出方程中的待定系数，进而可得所求的方程；（2）由直线和圆相切可得(t≠0)，然后将直线方程代入椭圆方程后得到关于x的一元二次方程，根据根据系数的关系可得点C的坐标，代入椭圆方程后整理得到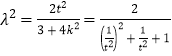，根据的范围可得，进而得到所求范围．

（1）设椭圆的标准方程为，

由已知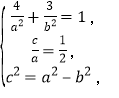得解得

所以椭圆的标准方程为.

（2）因为直线：y＝kx＋t与圆(x－1)2＋y2＝1相切，

所以＝1，

整理得(t≠0)．

由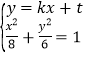消去y整理得(3＋4k2)x2＋8ktx＋4t2－24＝0，

因为直线与椭圆交于M，N两点，

所以，

将代入上式可得恒成立．

设M(x1，y1)，N(x2，y2)，

则有x1＋x2＝－，

所以y1＋y2＝kx1＋t＋kx2＋t＝k(x1＋x2)＋2t＝，

因为 )，

所以可得C，

又因为点C在椭圆上，

所以＋＝1,

所以，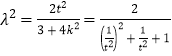

因为t2＞0，所以＋＋1＞1，

所以，

所以的取值范围为.