题目内容
下列函数中,既是偶函数又在区间(0,+ )上单调递减的是( )
)上单调递减的是( )
| A.y=-ln|x| | B.y=x3 | C.y=2|x| | D.y=cosx |
A
解析试题分析:y= -ln|x|是偶函数,且在区间(0,+ )上单调递减,故A正确;y=x3是奇函数且在区间(0,+
)上单调递减,故A正确;y=x3是奇函数且在区间(0,+ )上单调递增,故B不正确;y=2|x|是偶函数且在区间(0,+
)上单调递增,故B不正确;y=2|x|是偶函数且在区间(0,+ )上单调递增,故C不正确;y=cosx是偶函数但在区间(0,+
)上单调递增,故C不正确;y=cosx是偶函数但在区间(0,+ )上不具有单调性,故D不正确。
)上不具有单调性,故D不正确。
考点:1函数奇偶性;2函数单调性。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知函数 的导函数
的导函数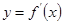 的图象如图所示,则关于函数
的图象如图所示,则关于函数 ,下列说法正确的是 ( )
,下列说法正确的是 ( )
A.在 处取得最大值 处取得最大值 | B.在区间 上是增函数 上是增函数 |
C.在区间 上函数值均小于0 上函数值均小于0 | D.在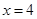 处取得极大值 处取得极大值 |
函数 在
在 上是增函数,则实数
上是增函数,则实数 的范围是( )
的范围是( )
A. ≥ ≥ | B. ≥ ≥ | C. ≤ ≤ | D. ≤ ≤ |
下列函数 中,满足“对任意的
中,满足“对任意的 时,均有
时,均有 ”的是( )
”的是( )
A. | B. | C.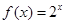 | D.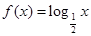 |
已知 是定义在
是定义在 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的 都满足
都满足 ,则
,则 是
是
| A.奇函数 | B.偶函数 |
| C.不是奇函数也不是偶函数 | D.既是奇函数又是偶函数 |
已知函数
 满足
满足 ,且
,且 时,
时, ,则当
,则当 时,
时, 与
与 的图象的交点个数为( )
的图象的交点个数为( )
| A.13 | B.12 | C.11 | D.10 |
方程 的解的个数为( )
的解的个数为( )
| A.1 | B.3 | C.4 | D.5 |
函数 的定义域为( )
的定义域为( )
A. | B. |
C. | D. |
 的函数,若存在距离为
的函数,若存在距离为 的两条平行直线
的两条平行直线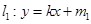 和
和 ,使得当
,使得当 时,
时, 恒成立,则称函数
恒成立,则称函数 在
在 ;②
;② ;③
;③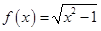 ;④
;④ .其中在
.其中在 上通道宽度为
上通道宽度为 的函数是( )
的函数是( )