题目内容
下列函数
中，满足“对任意的
时，均有
”的是（ ）
A． | B． | C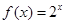． | D． |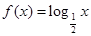
C
解析试题分析：因为函数满足“对任意的时，均有.等价于
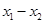与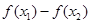
的值的正负号相同.即可化为
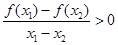.表示函数在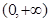
上的单调递增，由此可得只有函数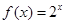符合.故选C.
考点：1.函数的单调性.2.斜率与函数的单调性的关系.
练习册系列答案
相关题目
的周长和面积同时分为相等的两部分的函数称为圆
函数
( )
A．是奇函数，且在 上是减函数 |
| B．是奇函数，且在上是增函数 |
| C．是偶函数，且在上是减函数 |
| D．是偶函数，且在上是增函数 |
已知
是函数
的一个零点.若
，则 ( )
A． | B． |
C． | D． |
下列函数中定义域为R，且是奇函数的是( )
A． =x2+x | B．=tanx |
| C．=x+sinx | D．= |
的图象大致是（ ）
下列函数中，既是偶函数又在区间（0，+
）上单调递减的是（ ）
| A．y=-ln|x| | B．y=x3 | C．y=2|x| | D．y=cosx |
函数
的定义域是（ ）
A． | B． |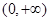
C． | D． |
是
上的奇函数，当
时，
，则当
时，
（ ）
A． | B． |
C． | D． |