题目内容
对定义域为 的函数,若存在距离为
的函数,若存在距离为 的两条平行直线
的两条平行直线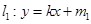 和
和 ,使得当
,使得当 时,
时, 恒成立,则称函数
恒成立,则称函数 在
在 有一个宽度为
有一个宽度为 的通道.有下列函数:①
的通道.有下列函数:① ;②
;② ;③
;③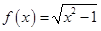 ;④
;④ .其中在
.其中在 上通道宽度为
上通道宽度为 的函数是( )
的函数是( )
| A.①③ | B.②③ | C.②④ | D.①④ |
A
解析试题分析:对于①中的函数 ,当
,当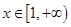 时,
时,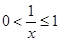 ,即
,即 ,取直线
,取直线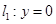 与
与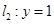 即可,故函数
即可,故函数 是在
是在 上通道宽度为
上通道宽度为 的函数;对于②中的函数
的函数;对于②中的函数 ,当
,当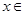
 时,结合图象可知,不存在距离为
时,结合图象可知,不存在距离为 的两条平行直线
的两条平行直线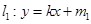 和
和 ,使得当
,使得当 时,
时, 恒成立,故②中的函数
恒成立,故②中的函数 不是在
不是在 上通道宽度为
上通道宽度为 的函数;对于③中的函数
的函数;对于③中的函数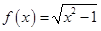 ,当
,当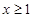 时,函数
时,函数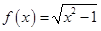 的图象表示的是双曲线
的图象表示的是双曲线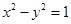 在第一象限内的图象,其渐近线方程为
在第一象限内的图象,其渐近线方程为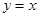 ,可取直线
,可取直线 和直线
和直线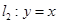 ,则有
,则有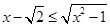
 在
在 上恒成立,故函数
上恒成立,故函数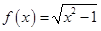 是在
是在 上通道宽度为
上通道宽度为 的函数;对于④中的函数
的函数;对于④中的函数
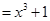 ,函数
,函数 在
在 上增长速度较一次函数快,结合图象可知,不存在距离为
上增长速度较一次函数快,结合图象可知,不存在距离为 的两条平行直线
的两条平行直线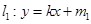 和
和 ,使得当
,使得当 时,
时, 恒成立,故④中的函数
恒成立,故④中的函数 不是在
不是在 上通道宽度为
上通道宽度为 的函数.故选A.
的函数.故选A.
考点:1.新定义;2.函数的图象

练习册系列答案
相关题目
下列函数在 上单调递增的是( )
上单调递增的是( )
A. | B. | C. | D. |
下列函数中定义域为R,且是奇函数的是( )
A. =x2+x =x2+x | B. =tanx =tanx |
C. =x+sinx =x+sinx | D. = = |
下列函数中,既是偶函数又在区间(0,+ )上单调递减的是( )
)上单调递减的是( )
| A.y=-ln|x| | B.y=x3 | C.y=2|x| | D.y=cosx |
函数 的定义域是( )
的定义域是( )
A. | B.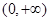 |
C. | D. |
定义在R上的函数 在(6, +∞)上为减函数,且函数y=f(x+6)为偶函数,则( )
在(6, +∞)上为减函数,且函数y=f(x+6)为偶函数,则( )
| A.f(4)>f(5) | B.f(4)>f(7) | C.f(5)>f(7) | D.f(5)>f(8) |
函数 图象交点的横坐标所在区间是( )
图象交点的横坐标所在区间是( )
| A.(1,2) | B.(2,3) | C.(3,4) | D.(1,5) |
 的图像可能是( )
的图像可能是( )
 ∠AMP(
∠AMP( ),练车时间为t,则函数
),练车时间为t,则函数 =
= 的图像大致为( )
的图像大致为( )