题目内容
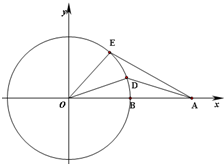 如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π
如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π(Ⅰ)当∠BOD=
| π | 6 |
(Ⅱ)将D、E两点间的距离用f(θ)表示,并求f(θ)的单调区间.
分析:(Ⅰ)由SODAE=S△OAE-S△OAD,关键分别求出相应三角形的面积;(Ⅱ)由条件点D,E都从点B同时出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍,用坐标表示点,从而表达出f(θ)表示,再求f(θ)的单调区间.
解答:解:(Ⅰ)当∠BOD=
时,∠BOE=
即D(
,
),E(
,
)SODAE=S△OAE-S△OAD=
×2×
-
×2×
=
;
(Ⅱ)∵点D,E都从点B同时出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.
∴∠BOE=2∠BOD,∠BOD=θ,∠BOE=2θ,0≤θ<2π
由三角函数的定义可知,点D(cosθ,sinθ),E(cos2θ,sin2θ)
f(θ)=
=
=
=2|sin
|
∵0≤θ<2π,∴0≤
<π,sin
≥0,∴f(θ)=2sin
由0≤
≤
得:0≤θ≤π,由
<
<π得:π<θ<2π
∴f(θ)的单调递增区间是[0,π],单调递减区间是(π,2π).
| π |
| 6 |
| π |
| 3 |
即D(
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)∵点D,E都从点B同时出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.
∴∠BOE=2∠BOD,∠BOD=θ,∠BOE=2θ,0≤θ<2π
由三角函数的定义可知,点D(cosθ,sinθ),E(cos2θ,sin2θ)
f(θ)=
| (cos2θ-cosθ)2+(sin2θ-sinθ)2 |
| 2-2(cos2θcosθ+sin2θsinθ) |
| 2(1-cosθ) |
| θ |
| 2 |
∵0≤θ<2π,∴0≤
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
由0≤
| θ |
| 2 |
| π |
| 2 |
| π |
| 2 |
| θ |
| 2 |
∴f(θ)的单调递增区间是[0,π],单调递减区间是(π,2π).
点评:本题主要考查再实际问题中建立三角函数模型,考查三角函数的定义及化简,有一定的综合性.

练习册系列答案
相关题目
 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C. 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
 ,求四边形ODAE的面积;
,求四边形ODAE的面积;