题目内容
已知函数![]()
![]()
(I)若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(II)若![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)因为![]() ,分
,分
由![]() 即
即![]() 得
得![]() ,
,
所以![]() 的解析式为
的解析式为![]() .
.
(Ⅱ)若![]() ,则
,则![]() ,
,![]() ,
,
(1)当![]() ,即
,即![]() 时,
时,![]() 恒成立,那么
恒成立,那么![]() 在
在![]() 上单调递增,
上单调递增,
所以,当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(2)解法1:当![]() ,即
,即![]() 或
或![]() 时,
时,
令![]() 解得
解得![]() ,
,![]()
列表分析函数![]() 的单调性如下:
的单调性如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
要使函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
只需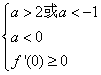 或
或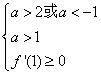 ,
,
解得![]() 或
或![]() .
.
解法2:当![]() ,即
,即![]() 或
或![]() 时,
时,
因为![]() 的对称轴方程为
的对称轴方程为![]()
要使函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
需![]() 或
或![]()
解得![]() 或
或![]() .
.
综上:当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目

 在
在 时取得极值,求实数
时取得极值,求实数 的值;
的值;

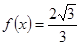 ,求sin2x的值;
,求sin2x的值; 的最大值与单调递增区间.
的最大值与单调递增区间.
 满足
满足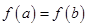 ,求
,求 的取值范围;
的取值范围; ,使得集合
,使得集合 ,如果存在,请求出
,如果存在,请求出 的取值范围;反之,请说明理由.
的取值范围;反之,请说明理由.
 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数 (
( 是自然常数)时,函数
是自然常数)时,函数
 .
.