题目内容
(本题满分13分)已知函数
(I)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(II)令 ,是否存在实数
,是否存在实数 ,当
,当 (
( 是自然常数)时,函数
是自然常数)时,函数
的最小值是3若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(改编)(Ⅲ)当 时,证明:
时,证明: .
.
【答案】
解:(I) 在
在 上恒成立,
上恒成立,
令 ,有
,有 得
得 ………………3分
………………3分
得 ………………4分
………………4分
(II) 假设存在实数 ,使
,使 ,
, 有最小值3,
有最小值3,
 ………………5分
………………5分
① 当 时,
时, 在
在 上单调递减,
上单调递减,
 ,
, (舍去),………………6分
(舍去),………………6分
②当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增

 ,
, ,满足条件.………………7分
,满足条件.………………7分
③ 当 时,
时, 在
在 上单调递减,
上单调递减,
 ,
, (舍去),………………8分
(舍去),………………8分
综上,存在实数 ,使得当
,使得当 时
时 有最小值3. ………………9分
有最小值3. ………………9分
(3)令 ,由(II)知
,由(II)知 .………………10分
.………………10分
令 ,
, ,
,
当 时,
时, ,
, 在
在 上单调递增
上单调递增
∴ ………………12分
………………12分
 即
即 .………………13分
.………………13分
【解析】略

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.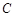 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.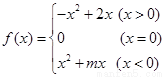 为奇函数;
为奇函数; 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.