题目内容
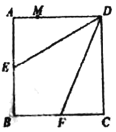
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,将
的中点,将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于
两点重合于![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)点![]() 是
是![]() 上一点,若
上一点,若![]() 平面
平面![]() ,则
,则![]() 为何值?并说明理由.
为何值?并说明理由.
(3)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见详解;(2)![]() ,理由见详解;(3)
,理由见详解;(3)![]() .
.
【解析】
(1)通过证明EF![]() 平面PBD,即可证明
平面PBD,即可证明![]() ;
;
(2)通过线面平行,将问题转化为线线平行,在平面图形中根据线段比例进而求解;
(3)根据(1)(2)所得,找到二面角的平面角,然后再进行求解.
(1)证明:因为四边形ABCD为正方形,
故DA![]() AE,DC
AE,DC![]() ,即折叠后的DP
,即折叠后的DP![]()
又因为![]() 平面PEF,
平面PEF,![]() 平面PEF,
平面PEF,![]()
故DP![]() 平面PEF,又
平面PEF,又![]() 平面PEF,故
平面PEF,故![]() .
.
在正方形ABCD中,容易知EF![]() ,
,
又![]() 平面PBD,
平面PBD,![]() 平面PBD,
平面PBD,![]()
故EF![]() 平面PBD,又
平面PBD,又![]() 平面PBD
平面PBD
故![]() ,即证.
,即证.
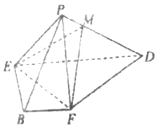
(2)连接BD交EF于O,连接OM,作图如下

因为![]() //平面
//平面![]() ,
,![]() 平面PBD,平面PBD
平面PBD,平面PBD![]() 平面
平面![]() =MO
=MO
故![]() //MO
//MO
在![]() 中,由
中,由![]() ,以及E、F分别是正方形ABCD两边的中点,
,以及E、F分别是正方形ABCD两边的中点,
故可得![]()
![]() 即为所求.
即为所求.
(3)过M作MH垂直于BD,垂足为H,连接OP,作图如下:

由(1)可知:EF![]() 平面PBD,因为MH
平面PBD,因为MH![]() 平面PBD,故EF
平面PBD,故EF![]()
又![]() ,
,![]() 平面EDF,BD
平面EDF,BD![]() 平面EDF,故MH
平面EDF,故MH![]() 平面EDF,
平面EDF,
又因为BD![]() EF,故
EF,故![]() 即为所求二面角的平面角.
即为所求二面角的平面角.
设正方形ABCD的边长为4,因为![]() ,故PM=1,
,故PM=1,
故在![]() 中,PM=1,EP=2,根据勾股定理可得ME
中,PM=1,EP=2,根据勾股定理可得ME![]()
同理:在![]() 中,PM=1,PF=2,根据勾股定理可得MF=
中,PM=1,PF=2,根据勾股定理可得MF=![]()
又EF=![]()
故在等腰三角形EMF中,因为O是EF的中点,故MO=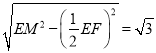 .
.
由(1)可知,PD![]() 平面PEF,又OP
平面PEF,又OP![]() 平面PEF,故PD
平面PEF,故PD![]() OP,
OP,
则![]() ,故可得
,故可得![]() ,
,
又在![]() 中,PE=PF=2,EF=2
中,PE=PF=2,EF=2![]() ,O为斜边EF上的中点,故OP=
,O为斜边EF上的中点,故OP=![]() ,
,
又因为MD=3,OD=![]()
故可解得MH=![]()
故在![]() 中,MH=1,MO=
中,MH=1,MO=![]() ,由勾股定理可得OH=
,由勾股定理可得OH=![]()
故![]() .
.
故二面角![]() 的余弦值为
的余弦值为![]() .
.

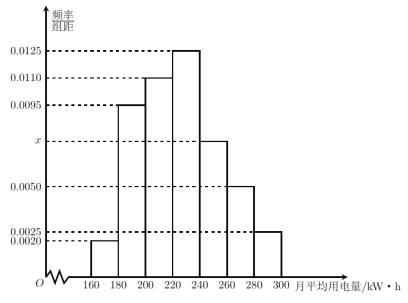
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:
收看时间(单位:小时) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
收看人数 | 14 | 30 | 16 | 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
体育达人 | 40 | ||
非体育达人 | 30 | ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.求抽取的这两人恰好是一男一女的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
参考公式:回归直线![]() ,其中
,其中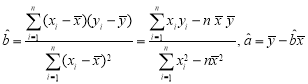 .
.