题目内容

O是平面上一定点，A，B，C平面上不共线的三个点，动点P满足
OP
=
OA
+λ(
AB
|
AB
|∠cosABC
+
AC
|
AC
|cos∠BCA
)，λ∈R，则P的轨迹一定通过△ABC的（　　）
A、外心B、内心C、重心D、垂心
分析：作数量积
BC
•
AB
|
AB
|cos∠ABC
=
|
BC
| |
AB
|cos(π-B)
|
AB
|cos∠ABC
=-|
BC
|，同理
BC
•
AC
|
AC
|cos∠ACD
=|
BC
|．
由于动点P满足
OP
=
OA
+λ(
AB
|
AB
|∠cosABC
+
AC
|
AC
|cos∠BCA
)，λ∈R．可得
AP
=λ(
AB
|
AB
|cos∠ABC
+
AC
|
AC
|cos∠ACD
)，λ∈R．得到
AP
•
BC
=λ(
BC
•
AB
|
AB
|cos∠ABC
+
BC
•
AC
|
AC
|cos∠ACD
)=0，即可判断出．
解答：解：如图所示，过点A作AD⊥BC，垂足为D点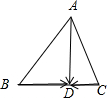．精英家教网
则
BC
•
AB
|
AB
|cos∠ABC
=
|
BC
| |
AB
|cos(π-B)
|
AB
|cos∠ABC
=-|
BC
|，
同理
BC
•
AC
|
AC
|cos∠ACD
=|
BC
|，
∵动点P满足
OP
=
OA
+λ(
AB
|
AB
|∠cosABC
+
AC
|
AC
|cos∠BCA
)，λ∈R．
∴
AP
=λ(
AB
|
AB
|cos∠ABC
+
AC
|
AC
|cos∠ACD
)，λ∈R．
∴
AP
•
BC
=λ(
BC
•
AB
|
AB
|cos∠ABC
+
BC
•
AC
|
AC
|cos∠ACD
)=λ(-|
BC
|+|
BC
|)=0，
∴
AP
⊥
BC
，
因此P的轨迹一定通过△ABC的垂心．
故选：D．
点评：本题考查了数量积运算、三角形的垂心性质，属于中档题．
练习册系列答案
相关题目
O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足
OP
=
OA
+λ(
AB
|
AB
|
+
AC
|
AC
|
)，λ∈[0，+∞），则P的轨迹一定通过△ABC的（　　）
A、外心B、内心C、重心D、垂心
O是平面上一定点，A，B，C是平面上不共线的三个点，动点P满足
OP
=
OA
+λ(
AB
|
AB
|
+
AC
|
AC
|
)，λ∈[0，+∞)，则P的轨迹一定通过△ABC的
 
心．
O是平面上一定点，A，B，C是平面上不共线的三个点，动点P满足
OP
=
OA
+λ(
AB
+
AC
)，λ∈[0，+∞），则P的轨迹一定通过△ABC的
 
心．
已知O是平面上一定点，A﹑B﹑C是平面上不共线的三个点，动点P满足
OP
=
OA
+λ（
AB
|
AB
|sinB
+
AC
|
AC
| sinC
）λ∈[0，+∞），则点P的轨迹一定通过△ABC的（　　）
A、外心B、内心C、重心D、垂心
O是平面上一定点，A，B，C是平面上不共线的三个点，动点P满足
OP
=
OA
+λ(
AB
+
AC
)，λ∈[0，+∞），则P的轨迹一定通过△ABC的（　　）
A、外心B、垂心C、内心D、重心

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网