题目内容
已知O是平面上一定点，A﹑B﹑C是平面上不共线的三个点，动点P满足
=
+λ（
+
）λ∈[0，+∞），则点P的轨迹一定通过△ABC的（ ）
| OP |
| OA |
| ||
|
|
| ||
|
|
| A、外心 | B、内心 | C、重心 | D、垂心 |
分析：将|
|sinB=|
|sinC提取出来，转化成λt（
+
），而λt（
+
）表示与
共线的向量，点D是BC的中点，故P的轨迹一定通过三角形的重心．
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AD |
解答：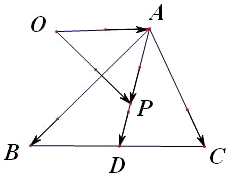
解：∵|
|sinB=|
|sinC设它们等于
∴
=
+λ•
（
+
）
而
+
=2
λ•
（
+
）表示与
共线的向量
而点D是BC的中点，所以即P的轨迹一定通过三角形的重心．故选C
解：∵|| AB |
| AC |
| 1 |
| t |
∴
| OP |
| OA |
| 1 |
| t |
| AB |
| AC |
而
| AB |
| AC |
| AD |
λ•
| 1 |
| t |
| AB |
| AC |
| AD |
| AP |
而点D是BC的中点，所以即P的轨迹一定通过三角形的重心．故选C
点评：本题主要考查了空间向量的加减法，以及三角形的三心等知识，属于基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
，l∈[0，+∞)．则P点的轨迹一定通过△ABC的( )
＝
＋λ(
＋
)，λ∈[0，＋∞)，则点P的轨迹一定通过△ABC的( )
则P点的轨迹一定通过△ABC的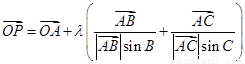
，
，则点P的轨迹一定通过
的（ ）