题目内容
 (2006•浦东新区模拟)已知曲线C:x2-y|y|=1(|x|≤4).
(2006•浦东新区模拟)已知曲线C:x2-y|y|=1(|x|≤4).(1)画出曲线C的图象,
(2)若直线l:y=kx-1与曲线C有两个公共点,求k的取值范围;
(3)若P(0,p)(p>0),Q为曲线C上的点,求|PQ|的最小值.
分析:(1)当y>0时,x2-y2=1;当y≤0时,x2+y2=1.利用等轴双曲线和单位圆即可得出,如图所示.
(2)若l:y=kx-1与x2+y2=1(y≤0)有两个公共点,利用图形即可得出.若l:y=kx-1与x2-y2=1(y>0)恰有一个公共点时,直线l:y=kx-1与曲线C也有两个公共点,联立方程,令△=0即可得出.
(3)分y>0与y≤0两种情况,利用两点间的距离公式和二次函数的单调性即可得出.
(2)若l:y=kx-1与x2+y2=1(y≤0)有两个公共点,利用图形即可得出.若l:y=kx-1与x2-y2=1(y>0)恰有一个公共点时,直线l:y=kx-1与曲线C也有两个公共点,联立方程,令△=0即可得出.
(3)分y>0与y≤0两种情况,利用两点间的距离公式和二次函数的单调性即可得出.
解答:解:(1)当y>0时,x2-y2=1,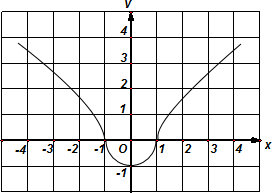
当y≤0时,x2+y2=1.如图所示.
(2)若l:y=kx-1与x2+y2=1(y≤0)有两个公共点,则k∈[-1,0)∪(0,1].
若l:y=kx-1与x2-y2=1(y>0)恰有一个公共点时,直线l:y=kx-1与曲线C也有两个公共点,
∴
⇒(1-k2)x2+2kx-2=0,
∴|k|>1,△=4k2+8(1-k2)=8-4k2=0,
解得 k=±
.
∴k的取值范围是{ -
}∪[ -1 , 0 )∪( 0 , 1 ]∪{
}.)
(3)当y≤0时,|PQ|2=x2+(y-p)2=1-2py+p2
由-1≤y≤0得,当y=0时| PQ |min=
.
当y>0时,|PQ|2=x2+(y-p)2=2y2-2py+p2+1=2 ( y-
p ) 2+
p2+1,
当y=
p时| PQ |min=
.
由于
>
∴|PQ|的最小值是
.

当y≤0时,x2+y2=1.如图所示.
(2)若l:y=kx-1与x2+y2=1(y≤0)有两个公共点,则k∈[-1,0)∪(0,1].
若l:y=kx-1与x2-y2=1(y>0)恰有一个公共点时,直线l:y=kx-1与曲线C也有两个公共点,
∴
|
∴|k|>1,△=4k2+8(1-k2)=8-4k2=0,
解得 k=±
| 2 |
∴k的取值范围是{ -
| 2 |
| 2 |
(3)当y≤0时,|PQ|2=x2+(y-p)2=1-2py+p2
由-1≤y≤0得,当y=0时| PQ |min=
| 1+p2 |
当y>0时,|PQ|2=x2+(y-p)2=2y2-2py+p2+1=2 ( y-
| 1 |
| 2 |
| 1 |
| 2 |
当y=
| 1 |
| 2 |
1+
|
由于
| 1+p2 |
1+
|
∴|PQ|的最小值是
1+
|
点评:本题综合考查了等轴双曲线和单位圆的标准方程及其性质、直线与曲线相交于相切的性质、数形结合思想方法、二次函数的单调性、斜率计算公式等基础知识与基本方法、基本技能,考查了推理能力和计算能力、解决问题的能力.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目