题目内容
一个正三棱柱恰好有一个内切球(球与三棱柱的两个底面和三个侧面都相切)和一个外接球(球经过三棱柱的6个顶点),则此内切球与外接球表面积之比为 .
1:5
设正三棱柱底面正三角形的边长为a,当球外切于正三棱柱时,球的半径R1等于正三棱柱的底面正三角形的边心距,求出正三棱柱的高为,当球外接正三棱柱时,球的圆心是正三棱柱高的中点,且球的圆心与正三棱柱两个底面正三角形构成两个正三棱锥,求出外接球的半径,即可求出内切球与外接球表面积之比.
解答:解:设正三棱柱底面正三角形的边长为a,其内切球的半径为R
当球外切于正三棱柱时,球的半径R等于正三棱柱的底面正三角形的重心到对边的距离即R=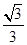 a,到相对棱的距离是
a,到相对棱的距离是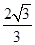 a
a
又正三棱柱的高是其内切球半径的2倍,故正三棱柱的高为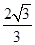 a,
a,
球外接正三棱柱时,球的圆心是正三棱柱高的中点,且球的圆心与正三棱柱两个底面正三角形构成两个正三棱锥,顶点在底面上的投影恰好是底面三角形的重心到顶点的距离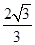 a,棱锥的高为
a,棱锥的高为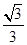 a
a
故正三棱锥外接球的半径满足R22=(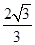 a)2+(
a)2+(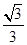 a)2=
a)2=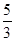 a2,
a2,
∴内切球与外接球表面积之比为4(πR2):(4πR22)=R2:R22=1:5.
故答案为1:5
解答:解:设正三棱柱底面正三角形的边长为a,其内切球的半径为R
当球外切于正三棱柱时,球的半径R等于正三棱柱的底面正三角形的重心到对边的距离即R=
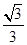 a,到相对棱的距离是
a,到相对棱的距离是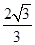 a
a又正三棱柱的高是其内切球半径的2倍,故正三棱柱的高为
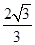 a,
a,球外接正三棱柱时,球的圆心是正三棱柱高的中点,且球的圆心与正三棱柱两个底面正三角形构成两个正三棱锥,顶点在底面上的投影恰好是底面三角形的重心到顶点的距离
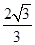 a,棱锥的高为
a,棱锥的高为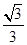 a
a故正三棱锥外接球的半径满足R22=(
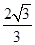 a)2+(
a)2+(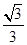 a)2=
a)2=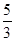 a2,
a2,∴内切球与外接球表面积之比为4(πR2):(4πR22)=R2:R22=1:5.
故答案为1:5

练习册系列答案
相关题目
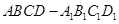 沿平面
沿平面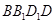 锯开后得到两个三棱柱,那么由这两个三棱柱组成的简单几何体有______________种,它们的表面积分别是_______________.(写出所有可能的情况,原正方体除外)
锯开后得到两个三棱柱,那么由这两个三棱柱组成的简单几何体有______________种,它们的表面积分别是_______________.(写出所有可能的情况,原正方体除外)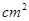 ,则长方体的体积是
,则长方体的体积是 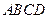 的外接球球心在
的外接球球心在 上,且
上,且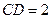 ,
,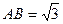 ,在外接球面上
,在外接球面上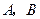 两点间的球面距离是 。
两点间的球面距离是 。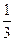
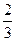
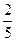
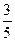

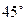 圈上有两点
圈上有两点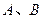 ,点
,点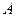 在东经
在东经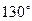 处,点
处,点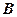 在西经
在西经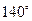 处,若地球半径为
处,若地球半径为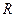 ,则
,则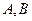 两点的球面距离为 ______________.
两点的球面距离为 ______________. 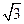 的矩形ABCD沿对角线AC折成直二面角B—AC—D且使A、B、C、D四点在同一球面上,则该球的体积为 ▲
的矩形ABCD沿对角线AC折成直二面角B—AC—D且使A、B、C、D四点在同一球面上,则该球的体积为 ▲ 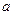 ,E,F,G,H分别是VA,VB,BC,AC的
,E,F,G,H分别是VA,VB,BC,AC的 __ 。
__ 。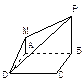
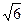 ,求这个正三棱锥的侧面积
,求这个正三棱锥的侧面积