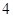题目内容
已知函数f(x)=ex,对于曲线y=f(x)上横坐标成等差数列的三个点A,B,C,给出以下判断:
①△ABC一定是钝角三角形
②△ABC可能是直角三角形
③△ABC可能是等腰三角形
④△ABC不可能是等腰三角形
其中,正确的判断是
| A.①③ | B.①④ | C.②③ | D.②④ |
B
解析试题分析:函数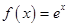 是增函数,对于曲线
是增函数,对于曲线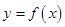 上横坐标成等差数列的三个点A,B,C,且横坐标依次增大,可得出∠ABC一定是钝角故①对,②错;由于由A到B的变化率要小于由B到C的变化率,由两点间距离公式可以得出AB<BC,故三角形不可能是等腰三角形,由此得出③不对,④对.
上横坐标成等差数列的三个点A,B,C,且横坐标依次增大,可得出∠ABC一定是钝角故①对,②错;由于由A到B的变化率要小于由B到C的变化率,由两点间距离公式可以得出AB<BC,故三角形不可能是等腰三角形,由此得出③不对,④对.
考点:函数图像及性质
点评:本题的求解要结合函数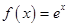 的图像及性质,通过观察图像可到角的范围,通过变化率得到边长间的大小关系
的图像及性质,通过观察图像可到角的范围,通过变化率得到边长间的大小关系

练习册系列答案
相关题目
已知f(x)=x3+x,若a,b,c∈R,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
| A.一定大于0 | B.一定等于0 | C.一定小于0 | D.正负都有可能 |
函数 的零点所在区间是( )
的零点所在区间是( )
A. | B.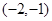  | C.(1,2) | D. |
下列函数中,既是奇函数又在区间(0.+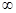 )上单调递增的函数是( )
)上单调递增的函数是( )
| A.y= 1nx | B.y=x3 | C.y=2| x| | D.y= sinx |
下列函数中既是奇函数,又在区间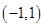 上是增函数的为( )
上是增函数的为( )
A.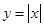 | B.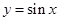 | C.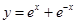 | D.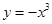 |
 在定义域内可导,
在定义域内可导, 图像如图所示,则导函数
图像如图所示,则导函数 的图像可能为( )
的图像可能为( )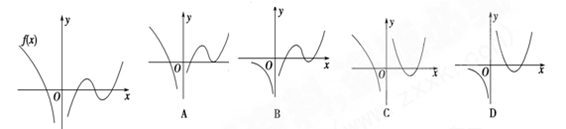
 的图象如图,那么导函数
的图象如图,那么导函数 的图象可能是( )
的图象可能是( )

 ,观察:
,观察: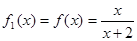 ,
,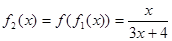 ,,
,, ,
, 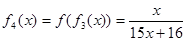 ……根据以上事实,由归纳推理可得当
……根据以上事实,由归纳推理可得当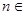 N*且
N*且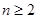 时,
时, 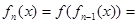 ( )
( )
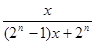
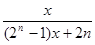
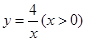 上,
上,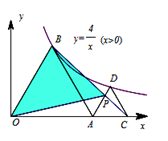
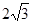 B.
B.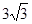 C.
C.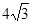 D.
D.