题目内容
下列函数中，既是奇函数又在区间（0．+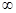
）上单调递增的函数是（ ）
| A．y= 1nx | B．y=x3 | C．y=2| x| | D．y= sinx |
B
解析试题分析：解：y=sinx为奇函数，但在[0，+∞]上不是单调函数；．y=2| x| 为偶函数,排除D,C,,对于函数A．y= 1nx 定义域为x>0,因此没有奇偶性，排除A，故选B.
考点：函数奇偶性
点评：本题考察了基本初等函数的图象和性质以及简单复合函数的性质，函数奇偶性的判断，函数单调性的判断方法
练习册系列答案
相关题目
函数
的值域是（ ）
A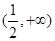． | B． | C． | D． |
函数
的最大值为
A． | B． | C． | D． |
已知函数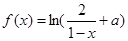
（
为常数）是奇函数，则实数为（ ）
| A．1 | B．—3 | C．3 | D．—1 |
已知函数f（x）=ex，对于曲线y=f（x）上横坐标成等差数列的三个点A,B,C，给出以下判断：
①△ABC一定是钝角三角形
②△ABC可能是直角三角形
③△ABC可能是等腰三角形
④△ABC不可能是等腰三角形
其中，正确的判断是
| A．①③ | B．①④ | C．②③ | D．②④ |
已知定义在R上的函数
满足
，如图表示该函数在区间
上的图象，则
等于
| A．3 | B．2 | C．1 | D．0 |
如图，在平面直角坐标系中，正六边形
的中心在坐标原点，边长为
，
平行于
轴，直线
(
为常数)与正六边形交于
两点，记
的面积为
，则关于函数
的奇偶性的判断正确的是（ ）
| A．一定是奇函数 | B．—定是偶函数 |
| C．既不是奇函数，也不是偶函数 | D．奇偶性与有关 |
若2x－3－x≥2－y－3y，则
| A．x－y≥0 | B．x－y≤0 | C．x＋y≥0 | D．x＋y≤0 |