题目内容
(2012•梅州二模)己知椭圆C:
+
=1(a>b>0)的离心率为
,不等式
+
≤1所表示的平面区域的面积为16
.
(1)求椭圆C的方程;
(2)设椭圆C上是否存在两个不同的点P,Q,使P,Q关于直线y=4x+m对称?若存在,求m的取值范围;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| |x| |
| a |
| |y| |
| b |
| 2 |
(1)求椭圆C的方程;
(2)设椭圆C上是否存在两个不同的点P,Q,使P,Q关于直线y=4x+m对称?若存在,求m的取值范围;若不存在,请说明理由.
分析:(1)根据椭圆C:
+
=1(a>b>0)的离心率为
,可得a=
b;利用不等式
+
≤1所表示的平面区域的面积为16
,可得4×
ab=16
,从而可得椭圆C的方程;
(2)假设P,Q存在,设出点的坐标,利用点差法可得PQ的中点M的坐标,根据M在椭圆内,建立不等式,即可求得m的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| |x| |
| a |
| |y| |
| b |
| 2 |
| 1 |
| 2 |
| 2 |
(2)假设P,Q存在,设出点的坐标,利用点差法可得PQ的中点M的坐标,根据M在椭圆内,建立不等式,即可求得m的取值范围.
解答:解:(1)∵椭圆C:
+
=1(a>b>0)的离心率为
,∴
=
,∴a=
b①
根据对称性知,不等式
+
≤1所表示的平面区域是椭圆C的四个顶点为顶点的菱形,可得4×
ab=16
②
由①②可得a=4,b=2
∴椭圆C的方程为
+
=1;
(2)假设P,Q存在,设P(x1,y1)、Q(x2,y2),PQ的中点M(x0,y0),则
两式相减可得
+
=1
∴
=-
×
=-
×
=-
∴y0=2x0
∵y0=4x0+m,∴x0=-
,y0=-m
∵M在椭圆内,∴
+
<1
∴
+
<1
∴m2<
∴-
<m<
∴m的取值范围是(-
,
).
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| a |
| ||
| 2 |
| 2 |
根据对称性知,不等式
| |x| |
| a |
| |y| |
| b |
| 1 |
| 2 |
| 2 |
由①②可得a=4,b=2
| 2 |
∴椭圆C的方程为
| x2 |
| 16 |
| y2 |
| 8 |
(2)假设P,Q存在,设P(x1,y1)、Q(x2,y2),PQ的中点M(x0,y0),则
|
两式相减可得
| x22-x12 |
| 16 |
| y22-y12 |
| 8 |
∴
| y2-y1 |
| x2-x1 |
| 8 |
| 16 |
| x1+x2 |
| y1+y2 |
| 1 |
| 2 |
| x0 |
| y0 |
| 1 |
| 4 |
∴y0=2x0
∵y0=4x0+m,∴x0=-
| m |
| 2 |
∵M在椭圆内,∴
| x02 |
| 16 |
| y02 |
| 8 |
∴
(-
| ||
| 16 |
| m2 |
| 8 |
∴m2<
| 64 |
| 9 |
∴-
| 8 |
| 3 |
| 8 |
| 3 |
∴m的取值范围是(-
| 8 |
| 3 |
| 8 |
| 3 |
点评:本题考查椭圆的标准方程,考查椭圆的对称性,考查点差法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
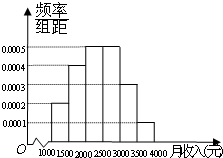 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).