题目内容
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (φ为参数,0≤φ≤π),曲线C2的参数方程为
(φ为参数,0≤φ≤π),曲线C2的参数方程为  (t为参数).
(t为参数).
(1)求C1的普通方程并指出它的轨迹;
(2)以O为极点,x轴的非负半轴为极轴建立极坐标系,射线OM:θ= ![]() 与半圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与半圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
【答案】
(1)解:曲线C1的参数方程为 ![]() (φ为参数,0≤φ≤π),
(φ为参数,0≤φ≤π),
消去参数φ可得普通方程:(x﹣2)2+y2=4.
∵0≤φ≤π,
∴0≤x≤4,0≤y≤2.
∴它表示上半圆,其图象在x轴的上方及其x轴上的两点(0,0),(4,0).
(2)解:由半圆C:(x﹣2)2+y2=4,(0≤y≤2)化为极坐标方程:ρ=4cosθ,θ∈ ![]() ,
,
把 ![]() 代入可得ρ=4
代入可得ρ=4 ![]() =2
=2 ![]() ,
,
∴|OP|=2 ![]() .
.
曲线C2的参数方程为 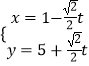 (t为参数),
(t为参数),
消去参数t化为普通方程:x+y=6,
可得极坐标方程:ρcosθ+ρsinθ=6,
把θ= ![]() 代入可得:ρ=
代入可得:ρ= ![]() =3
=3 ![]() =|OQ|.
=|OQ|.
∴|PQ|=|OQ|﹣|OP|=3 ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
【解析】(1)曲线C1的参数方程为 ![]() (φ为参数,0≤φ≤π),消去参数φ可得普通方程,注意y的取值范围.(2)由半圆C:(x﹣2)2+y2=4,(0≤y≤2)化为极坐标方程:ρ=4cosθ,θ∈
(φ为参数,0≤φ≤π),消去参数φ可得普通方程,注意y的取值范围.(2)由半圆C:(x﹣2)2+y2=4,(0≤y≤2)化为极坐标方程:ρ=4cosθ,θ∈ ![]() ,把
,把 ![]() 代入可得|OP|.曲线C2的参数方程为
代入可得|OP|.曲线C2的参数方程为 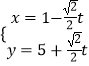 (t为参数),消去参数t化为普通方程,进而得到极坐标方程,把θ=
(t为参数),消去参数t化为普通方程,进而得到极坐标方程,把θ= ![]() 代入可得:|OQ|.利用|PQ|=|OQ|﹣|OP|即可得出.
代入可得:|OQ|.利用|PQ|=|OQ|﹣|OP|即可得出.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目