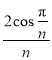Question

【题目】在①，②（），③（）这三个条件中任选一个，补充在下面的问题中，若问题中的k存在，求出k的值；若k不存在，说明理由.已知数列为等比数列，，，数列的首项，其前n项和为，______，是否存在，使得对任意，恒成立？

注：如果选择多个条件分别解答，按第一个解答计分.

Answer 1

【答案】见解析

【解析】

由数列为等比数列可得，①通过，整理可得，进而可求出数列的通项公式，求出，利用单调性可判断；②由可得数列为等比数列，求出数列的通项公式，求出，利用单调性可判断；③由知数列是等差数列，求出数列的通项公式，求出，利用作差法求最大项即可判断..

设等比数列的公比为q，因为，所以，

所以，

故.

若选择①，则，则（），两式相减整理得（），又，

所以是首项为1，公比为2的等比数列，所以

所以

由指数函数的性质知，数列单调递增，没有最大值，

所以不存在，使得对任意，恒成立.

若选择②，则由（），，知数列是首项为1，公比为的等比数列，

所以

所以

因为.当且仅当时取得最大值.

所以存在，使得对任意，恒成立.

若选择③，则由（）知数列是公差为2的等差数列.

又，所以.

设，

则

所以当时，，当时，.

即

所以存在，使得对任意，恒成立.