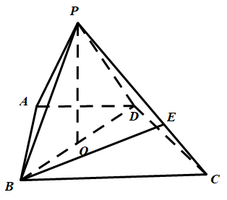
题目内容
【题目】已知椭圆![]() .双曲线
.双曲线![]() 的实轴顶点就是椭圆
的实轴顶点就是椭圆![]() 的焦点,双曲线
的焦点,双曲线![]() 的焦距等于椭圆
的焦距等于椭圆![]() 的长轴长.
的长轴长.
(1)求双曲线的标准方程;
(2)设直线![]() 经过点
经过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的面积的最大值;
的面积的最大值;
(3)设直线![]() (其中为
(其中为![]() 整数)与椭圆
整数)与椭圆![]() 交于不同两点
交于不同两点![]() ,与双曲线
,与双曲线![]() 交于不同两点
交于不同两点![]() ,问是否存在直线
,问是否存在直线![]() ,使得向量
,使得向量![]() ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
【答案】(1) ![]() (2)
(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)根据椭圆方程可以得到双曲线的焦距和顶点坐标,从而直接写出双曲线方程即可;
(2)设出直线方程,将三角形面积拆分为2个三角形的面积,从而利用韦达定理进行处理;
(3)根据直线与两个曲线相交,通过![]() 夹逼出
夹逼出![]() 的取值范围,再结合向量相加为零转化出的条件,得到
的取值范围,再结合向量相加为零转化出的条件,得到![]() 之间的关系,从而利用
之间的关系,从而利用![]() 是整数,对结果进行取舍即可.
是整数,对结果进行取舍即可.
(1)对椭圆![]() ,因为
,因为![]() ,
,
故其焦点为![]() ,椭圆的长轴长为
,椭圆的长轴长为![]() .
.
设双曲线方程为![]() ,
,
由题可知:![]() ,解得
,解得![]() .
.
故双曲线的方程为:![]() .
.
(2)因为直线AB的斜率显然不为零,
故设直线方程为![]() ,联立椭圆方程
,联立椭圆方程![]()
可得![]()
设交点![]() ,
,
则![]()
则![]()

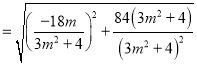

![]()
又![]()
故![]()
![]()
令![]() ,解得
,解得![]()
故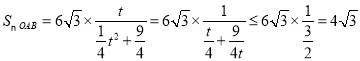
当且仅当![]() 时,即
时,即![]() 时,取得最大值.
时,取得最大值.
故![]() 的面积的最大值为
的面积的最大值为![]() .
.
(3)联立直线![]() 与椭圆方程
与椭圆方程![]()
可得![]()
![]()
整理得![]() ①
①
设直线与椭圆的交点为![]()
故可得![]() ②
②
同理:联立直线![]() 与双曲线方程
与双曲线方程![]()
可得![]()
![]()
整理得![]() ③
③
设直线与双曲线的交点为![]()
故可得![]() ④
④
要使得![]()
即可得![]()
故可得![]()
将②④代入可得![]()
解得![]() .
.
综上所述,要满足题意,只需使得:
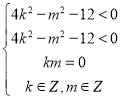
故当![]() 时,
时,![]() 可以取得
可以取得![]() 满足题意;
满足题意;
即直线方程可以为![]()
当![]() 时,
时,![]() 可以取
可以取![]() 满足题意.
满足题意.
即直线方程可以为![]()
故存在这样的直线有9条,能够使得![]() .
.

【题目】为了响应国家号召,某校组织部分学生参与了“垃圾分类,从我做起”的知识问卷作答,并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握认为“性别”与“问卷的结果”有关?
(2)在成绩合格的学生中,利用性别进行分层抽样,共选取9人进行座谈,再从这9人中随机抽取5人发送奖品,记拿到奖品的男生人数为X,求X的分布列及数学期望![]() .
.
附: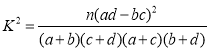
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |