题目内容
已知函数f（x）=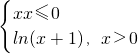
若f（2-x2）＞f（x），则实数x的取值范围是
- A.（-∞，-1）∪（2，+∞）
- B.（-∞，-2）∪（1，+∞）
- C.（-1，2）
- D.（-2，1）
D
分析：先通过基本函数得到函数的单调性，再利用单调性定义列出不等式，求出不等式的解集即可得到实数x的范围．
解答：易知f（x）在R上是增函数，
∵f（2-x2）＞f（x）
∴2-x2＞x，
解得-2＜x＜1．
则实数x的取值范围是（-2，1）．
故选D．
点评：本题主要考查利用函数的单调性来解不等式，这类题既考查不等式的解法，也考查了函数的性质，这也是函数方程不等式的命题方向，应引起足够的重视．
分析：先通过基本函数得到函数的单调性，再利用单调性定义列出不等式，求出不等式的解集即可得到实数x的范围．
解答：易知f（x）在R上是增函数，
∵f（2-x2）＞f（x）
∴2-x2＞x，
解得-2＜x＜1．
则实数x的取值范围是（-2，1）．
故选D．
点评：本题主要考查利用函数的单调性来解不等式，这类题既考查不等式的解法，也考查了函数的性质，这也是函数方程不等式的命题方向，应引起足够的重视．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、命题：“已知函数f（x），若f（x+1）与f（x-1）均为奇函数，则f（x）为奇函数，”为直命题 | B、“x＞1”是“|x|＞1”的必要不充分条件 | C、若“p且q”为假命题，则p，q均为假命题 | D、命题p：”?x∈R，使得x2+x+1＜0”，则?p：”?x∈R，均有x2+x+1≥0” |
，若f（a）=
，则实数a的值为（ ）
