题目内容
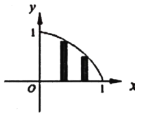
【题目】在平面直角坐标系中,函数![]() 在第一象限内的图像如图所示,试做如下操作,把
在第一象限内的图像如图所示,试做如下操作,把![]() 轴上的区间
轴上的区间![]() 等分成
等分成![]() 个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数![]() 的图像上.若用
的图像上.若用![]() ,表示第
,表示第![]() 个矩形的面积,
个矩形的面积,![]() 表示这
表示这![]() 个矩形的面积总和.
个矩形的面积总和.
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)请用数学归纳法证明等式:![]() ;
;
(Ⅲ)求![]() 的值,并说明
的值,并说明![]() 的几何意义.
的几何意义.
【答案】(Ⅰ) (Ⅱ)证明见解析(Ⅲ)
(Ⅱ)证明见解析(Ⅲ)![]() ,
,![]() 的几何意义表示函数
的几何意义表示函数![]() 的图象与
的图象与![]() 轴,及直线
轴,及直线![]() 和
和![]() 所围曲线梯形的面积.
所围曲线梯形的面积.
【解析】
(1)第![]() 个矩形的高为
个矩形的高为![]() ,然后直接求出第
,然后直接求出第![]() 个矩形的面积;
个矩形的面积;
(2)当![]() 时,命题成立,假设
时,命题成立,假设![]() 时命题成立,证得
时命题成立,证得![]() 时命题成立,即可得到结论;
时命题成立,即可得到结论;
(3)求得 ,求出极限,然后说明极限的几何意义.
,求出极限,然后说明极限的几何意义.
(Ⅰ)由题意第![]() 个矩形的高是
个矩形的高是![]() ,所以
,所以
(Ⅱ)(i)当![]() 时,
时,![]() ,命题成立,
,命题成立,
(ii)假设![]() 时命题成立,即
时命题成立,即![]() ,
,
则![]() 时,
时,![]()
![]() ,
,
∴![]() 时命题成立,
时命题成立,
综上,![]() 时,命题成真,即
时,命题成真,即![]() ,
,
(Ⅲ)由(1)可求得
![]() ,
,
则![]() ,
,
所以![]() 的几何意义表示函数
的几何意义表示函数![]() 的图象与
的图象与![]() 轴,及直线
轴,及直线![]() 和
和![]() 所围曲线梯形的面积为
所围曲线梯形的面积为![]() .
.

练习册系列答案
相关题目
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 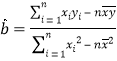 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?


