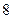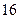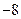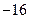题目内容
(本小题满分12分)
已知平面向量a=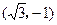 ,b=
,b=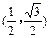
(1)证明a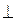 b;
b;
(2)若存在实数k,t,使x=a+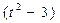 b,y=-ka+tb,且x
b,y=-ka+tb,且x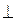 y,试求k,t的函数关系式
y,试求k,t的函数关系式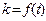 ;
;
(3)根据(2)的结论,讨论关于t的方程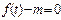 的解的情况。
的解的情况。
已知平面向量a=
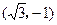 ,b=
,b=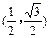
(1)证明a
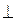 b;
b;(2)若存在实数k,t,使x=a+
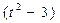 b,y=-ka+tb,且x
b,y=-ka+tb,且x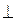 y,试求k,t的函数关系式
y,试求k,t的函数关系式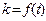 ;
;(3)根据(2)的结论,讨论关于t的方程
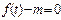 的解的情况。
的解的情况。(1) 略
(2) k=

(3)
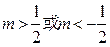 时,直线k=m与曲线
时,直线k=m与曲线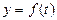 仅有一个交点,则方程有一解;
仅有一个交点,则方程有一解;当
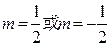 时,直线k=m与曲线
时,直线k=m与曲线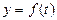 有两个交点,则方程有两解;
有两个交点,则方程有两解;当
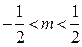 时,直线k=m与曲线
时,直线k=m与曲线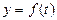 有三个交点,则方程有三个解。
有三个交点,则方程有三个解。解(1)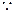 a·b
a·b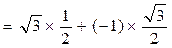 =0,
=0,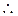 a
a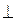 b。
b。
(2)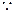 x
x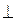 y,
y,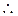 x·y=0,即〔a+
x·y=0,即〔a+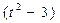 b〕·(—ka+tb)=0
b〕·(—ka+tb)=0
整理得-ka2+〔t-k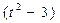 〕a·b+t
〕a·b+t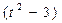 b2=0
b2=0
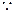 a·b=0,a2=4,b2=1。
a·b=0,a2=4,b2=1。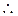 上式化为-4k+ t
上式化为-4k+ t 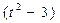 =0,
=0, k=
k=
(3)讨论方程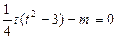 的解得情况,可以看做曲线
的解得情况,可以看做曲线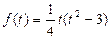 与直线k=m的交点个数。
与直线k=m的交点个数。
于是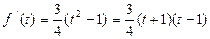 。
。
令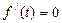 ,解得
,解得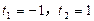 ,当
,当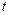 变化时,
变化时,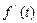 、
、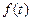 的变化情况如下表:
的变化情况如下表:
当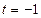 时,
时,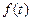 有极大值,极大值为
有极大值,极大值为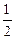 。
。
当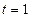 时,
时,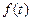 有极小值,极小值为
有极小值,极小值为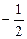 。
。
而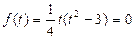 时,得
时,得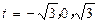 。 所以
。 所以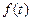 的图像大致如图所示
的图像大致如图所示
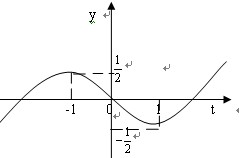
于是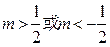 时,直线k=m与曲线
时,直线k=m与曲线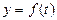 仅有一个交点,则方程有一解;
仅有一个交点,则方程有一解;
当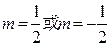 时,直线k=m与曲线
时,直线k=m与曲线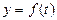 有两个交点,则方程有两解;
有两个交点,则方程有两解;
当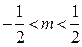 时,直线k=m与曲线
时,直线k=m与曲线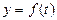 有三个交点,则方程有三个解。
有三个交点,则方程有三个解。
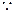 a·b
a·b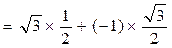 =0,
=0,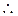 a
a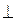 b。
b。(2)
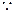 x
x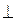 y,
y,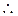 x·y=0,即〔a+
x·y=0,即〔a+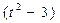 b〕·(—ka+tb)=0
b〕·(—ka+tb)=0整理得-ka2+〔t-k
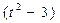 〕a·b+t
〕a·b+t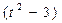 b2=0
b2=0 a·b=0,a2=4,b2=1。
a·b=0,a2=4,b2=1。 上式化为-4k+ t
上式化为-4k+ t 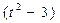 =0,
=0,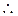 k=
k=
(3)讨论方程
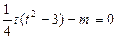 的解得情况,可以看做曲线
的解得情况,可以看做曲线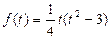 与直线k=m的交点个数。
与直线k=m的交点个数。于是
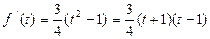 。
。令
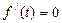 ,解得
,解得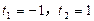 ,当
,当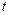 变化时,
变化时,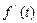 、
、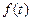 的变化情况如下表:
的变化情况如下表: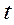 | 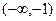 | 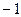 | 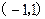 | 1 | 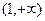 |
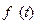 | 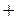 | 0 | - | 0 | + |
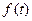 | 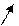 | 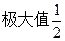 |  | 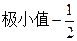 |  |
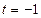 时,
时,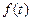 有极大值,极大值为
有极大值,极大值为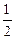 。
。当
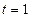 时,
时,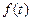 有极小值,极小值为
有极小值,极小值为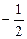 。
。而
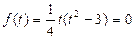 时,得
时,得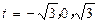 。 所以
。 所以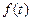 的图像大致如图所示
的图像大致如图所示
于是
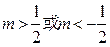 时,直线k=m与曲线
时,直线k=m与曲线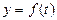 仅有一个交点,则方程有一解;
仅有一个交点,则方程有一解;当
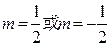 时,直线k=m与曲线
时,直线k=m与曲线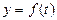 有两个交点,则方程有两解;
有两个交点,则方程有两解;当
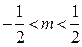 时,直线k=m与曲线
时,直线k=m与曲线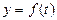 有三个交点,则方程有三个解。
有三个交点,则方程有三个解。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
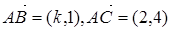 ,若
,若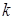 为满足
为满足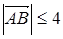 的一随机整数,则
的一随机整数,则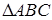 是直角三角形的概率为( )
是直角三角形的概率为( )
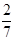
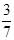
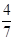
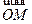 =2
=2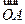 -
-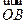 -
-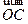 B、
B、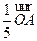 +
+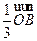 +
+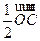
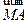 +
+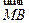 +
+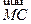 =
=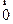 D、
D、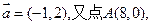
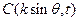
 与向量
与向量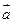 共线。
共线。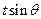 取最大值为4时,求
取最大值为4时,求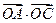 的值。
的值。 的外心, AB2, AC1,
的外心, AB2, AC1, , 设
, 设 ,若
,若 ,则
,则 __________________.
__________________.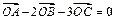 ,则
,则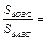 .
. 中,
中, ,斜坐标定义:如果
,斜坐标定义:如果 (其中
(其中 分别是
分别是 轴,
轴, 轴的单位向量),则
轴的单位向量),则 叫做
叫做 的斜坐标。已知
的斜坐标。已知 ),则
),则 =
= 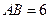 ,
,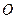 为圆心,
为圆心,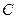 为半圆上不同于
为半圆上不同于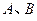 的任意一点,若
的任意一点,若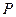 为半径
为半径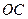 上的动点,则
上的动点,则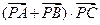 的最小值是___ _______.
的最小值是___ _______. 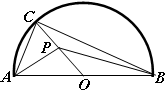
 ,
, 是
是 的垂直平分线,垂足
的垂直平分线,垂足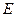 ,
,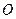 为直线
为直线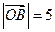 ,
,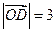 ,
,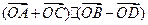 的值是( )
的值是( )