题目内容
50、设全集U是实数集R,M={x|x<-2或x>2},N={x|x2-4x+3<0},则图中阴影部分所表示的集合是( )


分析:由韦恩图表示集合的方法,分析图形中表示的阴影部分表示的几何意义,我们不难分析出阴影部分表示集合(CUM)∩N,然后结合M={x|x<-2或x>2},N={x|x2-4x+3<0},我们不难求出阴影部分所表示的集合.
解答:解:由图知,阴影部分表示集合(CUM)∩N,
由于M={x|x<-2或x>2},
∴CUM={x|-2<x<2},
N={x|1<x<3},
所以(CUM)∩N={x|1<x≤2}.
故选C
由于M={x|x<-2或x>2},
∴CUM={x|-2<x<2},
N={x|1<x<3},
所以(CUM)∩N={x|1<x≤2}.
故选C
点评:韦恩图是分析集合关系时,最常借助的工具,其特点是直观,要分析韦恩图分析阴影部分表示的集合,要先分析阴影部分的性质,先用自然语言将其描述出来,再根据集合运算的定义,将共转化为集合语言,再去利用集合运算的方法,对其进行变形和化简.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 设全集U是实数集R,M={x|x2>4},N={x|
设全集U是实数集R,M={x|x2>4},N={x|| 2 |
| x-1 |
| A、{x|-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|x<2} |
 设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )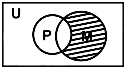 设全集U是实数集R,M={x|x<-1,或x>2},P={x|x<1或x>5},则图中阴部分所表示的集合是( )
设全集U是实数集R,M={x|x<-1,或x>2},P={x|x<1或x>5},则图中阴部分所表示的集合是( ) 设全集U是实数集R,
设全集U是实数集R, (2010•台州一模)设全集U是实数集R,M={x|x2>4},N={x|y=lg(x2-4x+3)},则图中阴影部分所表示的集合是
(2010•台州一模)设全集U是实数集R,M={x|x2>4},N={x|y=lg(x2-4x+3)},则图中阴影部分所表示的集合是