题目内容
已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AB=1,AD=2,F为CD的中点且AF∥平面BCE.
(I) 求线段DE的长;
(II) 求直线BF和平面BCE所成角的正切值.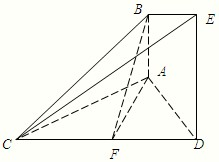
(I) 求线段DE的长;
(II) 求直线BF和平面BCE所成角的正切值.

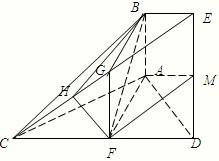
(I) 取CE的中点G,连FG、BG.
∵F为CD的中点,
∴GF∥DE且GF=
| 1 |
| 2 |
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB,
∴A,B,G,F四点共面.
又AF∥平面BCE,面ABGF∩面BCE=BG,
∴AF∥BG,∴四边形GFAB为平行四边形,
∴GF=AB.
∴DE=2AB=2.
(II)∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.
∵DE⊥平面ACD,AF?平面ACD,∴DE⊥AF.
又CD∩DE=D,故AF⊥平面CDE.
∵BG∥AF,∴BG⊥平面CDE.
∵BG?平面BCE,
∴平面BCE⊥平面CDE
在平面CDE内,过F作FH⊥CE于H,连BH.
∵平面BCE⊥平面CDE,∴FH⊥平面BCE.
∴∠FBH为BF和平面BCE所成的角.
在直角△BFH中,FH=CFsin45°=
| ||
| 2 |
| AB2+AF2 |
| 1+3 |
| ||
| 2 |
∴tan∠FBH=
| FH |
| BH |
| ||
| 7 |
∴直线BF和平面BCE所成角的正切值为
| ||
| 7 |

练习册系列答案
相关题目
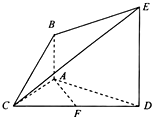 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.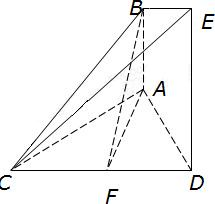 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. (2012•许昌二模)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•许昌二模)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.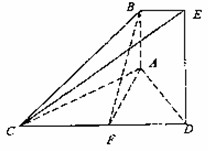 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ABC为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ABC为等边三角形,AD=DE=2AB,F为CD的中点.