题目内容
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点
(Ⅰ) 求证:平面BCE⊥平面CDE;
(Ⅱ) 求二面角B-EF-D的余弦值.
(Ⅰ) 求证:平面BCE⊥平面CDE;
(Ⅱ) 求二面角B-EF-D的余弦值.
分析:(1)设CE中点为M,连接BM,MF,则CB=BE,BM⊥CE,由MF
BA,知MB
FA,由此能够证明平面BCE⊥平面CDE.
(2)过M作MP⊥EF于P,连接BP,设底面正三角形边长为2,由BM⊥平面CDE,知BM⊥EF,由MP⊥EF,知EF⊥BP,所以∠BPM是二面角B-EF-D的平面角的补角,由此能求出二面角B-EF-D的余弦值.
| ∥ |
. |
| ∥ |
. |
(2)过M作MP⊥EF于P,连接BP,设底面正三角形边长为2,由BM⊥平面CDE,知BM⊥EF,由MP⊥EF,知EF⊥BP,所以∠BPM是二面角B-EF-D的平面角的补角,由此能求出二面角B-EF-D的余弦值.
解答: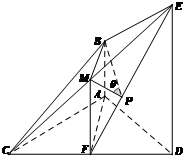 解:(1)设CE中点为M,连接BM,MF,则CB=BE,BM⊥CE,
解:(1)设CE中点为M,连接BM,MF,则CB=BE,BM⊥CE,
∵MF
BA,∴MB
FA,
∵DE⊥平面ACD,∴DE⊥AF,∴DE⊥BM,
又∵CE∩DE=E,∴BM⊥平面CDE,
又∵BM?平面BCE,
∴平面BCE⊥平面CDE.
(2)过M作MP⊥EF于P,连接BP,
设底面正三角形边长为2,
∵BM⊥平面CDE,∴BM⊥EF,
又∵MP⊥EF,∴EF⊥平面BMP,
∴EF⊥BP,
∴∠BPM是二面角B-EF-D的平面角的补角,
∵BM=
,MP=
,
∴cos∠BPM=
.
∴二面角B-EF-D的余弦值为-
.
 解:(1)设CE中点为M,连接BM,MF,则CB=BE,BM⊥CE,
解:(1)设CE中点为M,连接BM,MF,则CB=BE,BM⊥CE,∵MF
| ∥ |
. |
| ∥ |
. |
∵DE⊥平面ACD,∴DE⊥AF,∴DE⊥BM,
又∵CE∩DE=E,∴BM⊥平面CDE,
又∵BM?平面BCE,
∴平面BCE⊥平面CDE.
(2)过M作MP⊥EF于P,连接BP,
设底面正三角形边长为2,
∵BM⊥平面CDE,∴BM⊥EF,
又∵MP⊥EF,∴EF⊥平面BMP,
∴EF⊥BP,
∴∠BPM是二面角B-EF-D的平面角的补角,
∵BM=
| 3 |
| ||
| 5 |
∴cos∠BPM=
| 1 |
| 4 |
∴二面角B-EF-D的余弦值为-
| 1 |
| 4 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.