题目内容
【题目】已知点![]() ,点
,点![]() ,点
,点![]() ,动圆
,动圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (
(![]() 均不同于点
均不同于点![]() ),且
),且![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)证明:![]() 为定值,并求
为定值,并求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,当
两点,当![]() 三点共线时,求四边形
三点共线时,求四边形![]() 的面积.
的面积.
【答案】(1)证明见解析,方程为![]() .
.
(2) ![]() .
.
【解析】分析:(1)根据圆的切线性质可得,![]()
![]() ,从而根据椭圆的可得结果;(2)直线与曲线联立,利用韦达定理、弦长公式以及三角形面积公式可得四边形
,从而根据椭圆的可得结果;(2)直线与曲线联立,利用韦达定理、弦长公式以及三角形面积公式可得四边形![]() 的面积为
的面积为![]() .
.
详解:(1)由已知可得|PD|=|PE|,|BA|=|BD|,|CE|=|CA|,
所以|PB|+|PC|=|PD|+|DB|+|PC|
=|PE|+|PC|+|AB|
=|CE|+|AB|
=|AC|+|AB|=4>|BC|
所以点P的轨迹是以B,C为焦点的椭圆(去掉与x轴的交点),
可求的方程为![]() +
+![]() =1(y≠0).
=1(y≠0).
(2)由O,D,C三点共线及圆的几何性质,可知PB⊥CD,
又由直线CE,CA为圆O的切线,可知CE=CA,OA=OE,
所以△OAC≌△OEC,进而有∠ACO=∠ECO,
所以|PC|=|BC|=2,又由椭圆的定义,|PB|+|PC|=4,得|PB|=2,
所以△PBC为等边三角形,即点P在y轴上,点P的坐标为(0,±![]() )
)
(i)当点P的坐标为(0,![]() )时,∠PBC=60,∠BCD=30,
)时,∠PBC=60,∠BCD=30,
此时直线l1的方程为y=![]() (x+1),直线CD的方程为y=-
(x+1),直线CD的方程为y=-![]() (x-1),
(x-1),
由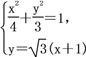 整理得5x2+8x=0,得Q(-
整理得5x2+8x=0,得Q(-![]() ,-
,-![]() ),所以|PQ|=
),所以|PQ|=![]() ,
,
由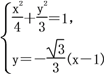 整理得13x2-8x-32=0,
整理得13x2-8x-32=0,
设M(x1,y1),N(x2,y2),x1+x2=![]() ,x1x2=-
,x1x2=-![]() ,
,
|MN|=![]() |x1-x2|=
|x1-x2|=![]() ,
,
所以四边形MPNQ的面积S=![]() |PQ|·|MN|=
|PQ|·|MN|=![]() .
.
(ii)当点P的坐标为(0,-![]() )时,由椭圆的对称性,四边形MPNQ的面积为
)时,由椭圆的对称性,四边形MPNQ的面积为![]() .
.
综上,四边形MPNQ的面积为![]() .
.

 名校课堂系列答案
名校课堂系列答案