题目内容
若圆（x-a）2+y2=2的圆心到直线x-y+1=0距离为
，则实数a等于（ ）
| 2 |
分析：利用圆（x-a）2+y2=2的圆心到直线x-y+1=0距离为
，建立方程，即可求得a的值．
| 2 |
解答：解：∵圆（x-a）2+y2=2的圆心到直线x-y+1=0距离为
，
∴d=
=
∴a=1或-3
故选B．
| 2 |
∴d=
| |a+1| | ||
|
| 2 |
∴a=1或-3
故选B．
点评：本题考查直线与圆的位置关系，解题的关键是利用圆心到直线的距离公式，属于基础题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
若圆（x-a）2+（y-a）2=4上，总存在不同两点到原点的距离等于1，则实数a的取值范围是（ ）
A、（
| ||||||||||||||||
B、（-
| ||||||||||||||||
C、（-
| ||||||||||||||||
D、（-
|
，则实数a等于（ ）
，
）
，-
）
，-
）∪（
，
）
，
）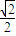