题目内容
若圆(x-a)2+(y-a)2=4上,总存在不同两点到原点的距离等于1,则实数a的取值范围是( )
A、(
| ||||||||||||||||
B、(-
| ||||||||||||||||
C、(-
| ||||||||||||||||
D、(-
|
分析:根据题意知:圆(x-a)2+(y-a)2=4和以原点为圆心,1为半径的圆x2+y2=1相交,因此两圆圆心距大于两圆半径之差、小于两圆半径之和,列出不等式,解此不等式即可.
解答:解:圆(x-a)2+(y-a)2=4和圆x2+y2=1相交,两圆圆心距d=
=
|a|,
∴2-1<
|a|<2+1 即:
<|a|<
,
∴-
<a<-
或
<a<
实数a的取值范围是 (-
,-
)∪(
,
)
故选C.
| (a-0)2+(a-0)2 |
| 2 |
∴2-1<
| 2 |
| ||
| 2 |
| 3 | ||
|
∴-
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
实数a的取值范围是 (-
| 3 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
故选C.
点评:本题体现了转化的数学思想,解题的关键在于将问题转化为:圆(x-a)2+(y-a)2=4和圆x2+y2=1相交,属中档题.

练习册系列答案
相关题目
 ,则实数a等于( )
,则实数a等于( ) ,
, )
) ,-
,- )
) ,-
,- )∪(
)∪( ,
, )
) ,
,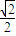 )
)