题目内容

函数f(x)=Asin(ωx-
π
6
)（A＞0，ω＞0）的最大值为2，其最小正周期为π．
（1）求函数f（x）的解析式；
（2）设α∈(0，
π
2
)，则f(
α
2
)=
2
，求cosα的值．
分析：（1）通过函数的最大值，求出A，函数的最小正周期求出ω，然后求出函数f（x）的解析式；
（2）根据α∈(0，
π
2
)，与f(
α
2
)=
2
，求出α-
π
6
的值，然后求出α的值，即可利用cosα通过两角和与差的余弦函数求出它的值．
解答：解：（1）由题意A=2，…（2分）
∵最小正周期T=π，∴ω=2…（4分）
故函数f（x）的解析式为f(x)=2sin(2x-
π
6
)…（5分）
（2）∵f(
α
2
)=2sin(2×
α
2
-
π
6
)=
2
，即sin(α-
π
6
)=
2
2
，…（6分）
∵0＜α＜
π
2
，∴-
π
6
＜α-
π
6
＜
π
3
，…（7分）
∴α-
π
6
=
π
4
，α=
π
6
+
π
4
，…（10分）
故cosα=cos(
π
6
+
π
4
)=cos
π
6
cos
π
4
-sin
π
6
sin
π
4
=
6
-
2
4
…（12分）
（或）∵0＜α＜
π
2
，∴-
π
6
＜α-
π
6
＜
π
3
，
∴cos(α-
π
6
)=
1-sin2(α-
π
6
)
=
2
2
，…（9分）
故cosα=cos[(α-
π
6
)+
π
6
]=cos(α-
π
6
)cos
π
6
-sin(α-
π
6
)sin
π
6
=
6
-
2
4
…（12分）
点评：本题考查三角函数的解析式的求法，两角和与差的三角函数的应用，函数值的求法，考查计算能力．
练习册系列答案
相关题目
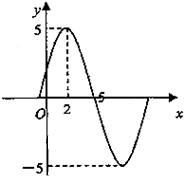精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）若图象g（x）与函数f（x）的图象关于点P（4，0）对称，求函数g（x）的单调递增区间．
（2013•大连一模）已知函数f(x)=Asin(ωx+φ)(x∈R，A＞0，ω＞0，|φ|＜
π
2
)的图象（部分）如图所示，则ω，φ分别为（　　）
当x∈[-
π
6
，
2π
3
]时，函数f(x)=Asin(ωx+θ) (A＞0，ω＞0，|θ|＜
π
2
)的图象如图所示．
（1）求函数f（x）在[-
π
6
，
2π
3
]上的表达式；
（2）求方程f(x)=
2
2
在[-
π
6
，
2π
3
]的解集．
精英家教网函数f(x)=Asin(ωx+φ)，x∈R(A＞0，ω＞0，|φ|＜
π
2
)的一段图象如图5所示：将y=f（x）的图象向右平移m（m＞0）个单位，可得到函数y=g（x）的图象，且图象关于原点对称，g(
π
2013
)＞0．
（1）求A、ω、φ的值；
（2）求m的最小值，并写出g（x）的表达式；
（3）若关于x的函数y=g(
tx
2
)在区间[-
π
3
，
π
4
]上最小值为-2，求实数t的取值范围．
精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，x∈R，|φ|＜
π
2
)的图象（部分）如图所示，则f（x）的解析式是（　　）
A、f(x)=5sin(
π
3
x+
π
6
)
B、f(x)=5sin(
π
6
x-
π
6
)
C、f(x)=5sin(
π
6
x+
π
6
)
D、f(x)=5sin(
π
3
x-
π
6
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网