题目内容
【题目】某中学从参加环保知识竟赛的学生中抽取了部分学生的成绩进行分析，不过作好的茎叶图和频率分布直方图因故均受到不同程度的损坏，其可见部分信息如图所示，据此解答下列问题：
（1）求抽取学生成绩的中位数，并修复频率分布直方图；
（2）根据修复的频率分布直方图估计该中学此次环保知识竞赛的平均成绩。（以各组的区间中点值代表该组的各个值）
【答案】（1）见解析（2）75
【解析】
（1）根据中位数定义得中位数应该是第10和第11个同学的成绩的平均数，再根据频数除以总数得频率，再除以组距得纵坐标，（2）根据组中值与对应概率乘积的和计算平均值.
解：（1）抽取的总人数为：
(人)
中位数应该是第10和第11个同学的成绩的平均数，
故：中位数
90-100的频率为：
60-70的频率为：
，即：
70-80的频率为：
，即：
80-90的频率为：
，即：
修复直方图如左图所示：
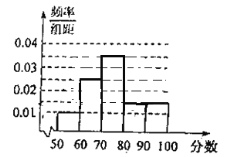
（2）
答：估计该中学此次环保知识竞赛的平均成绩是75分
黄冈天天练口算题卡系列答案【题目】某市为了宣传环保知识，举办了一次“环保知识知多少”的问卷调查活动（一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份， 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
（1）分别求出n， a， b， c的值；
（2）从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”，求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
【题目】已知圆
的圆心在直线
上，且圆经过点
与点
.
（1）求圆的方程；
（2）过点
作圆的切线，求切线所在的直线的方程.
【答案】（1）
；（2）
或
.
【解析】试题分析：（1）求出线段
的中点
，进而得到线段的垂直平分线为
，与
联立得交点
，∴
.则圆的方程可求
（2）当切线斜率不存在时，可知切线方程为.
当切线斜率存在时，设切线方程为
，由到此直线的距离为
，解得
，即可到切线所在直线的方程.
试题解析：（（1）设 线段的中点为，∵
，
∴线段的垂直平分线为，与联立得交点，
∴.
∴圆的方程为
.
（2）当切线斜率不存在时，切线方程为.
当切线斜率存在时，设切线方程为，即
，
则到此直线的距离为，解得
，∴切线方程为
.
故满足条件的切线方程为或.
【点睛】本题考查圆的方程的求法，圆的切线，中点弦等问题，解题的关键是利用圆的特性，利用点到直线的距离公式求解．
【题型】解答题
【结束】
20
【题目】某小型企业甲产品生产的投入成本
（单位：万元）与产品销售收入
（单位：万元）存在较好的线性关系，下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
（1）求
关于
的线性回归方程；
（2）根据（1）中的回归方程，判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大（
）？
相关公式： 
， 
.
