题目内容
(本小题满分14分)如图,在长方体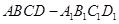 中,
中, ,
,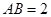 ,点
,点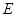 在棱
在棱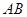 上移动.
上移动.
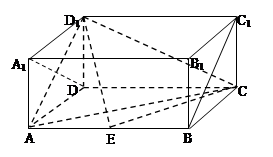
⑴ 证明: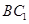 //平面
//平面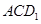 ;
;
⑵证明: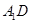 ⊥
⊥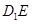 ;
;
⑶ 当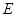 为
为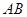 的中点时,求四棱锥
的中点时,求四棱锥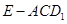 的体积.
的体积.
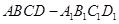 中,
中, ,
,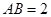 ,点
,点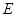 在棱
在棱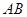 上移动.
上移动.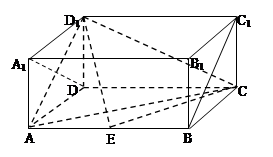
⑴ 证明:
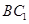 //平面
//平面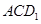 ;
;⑵证明:
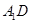 ⊥
⊥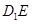 ;
;⑶ 当
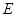 为
为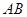 的中点时,求四棱锥
的中点时,求四棱锥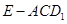 的体积.
的体积.(1)证明:见解析;(2) 证明:见解析;(3) E-ACD1的体积为 .
.
 .
. 试题分析:(1)利用线线平行的来证明线面平行。
(2)由AE⊥平面AA1DD1,A1D?平面AA1DD1,知A1D⊥AE,再由AA1DD1为正方形,利用直线与平面垂直的性质,能够证明A1D⊥D1E.
(3) 设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=
 ,AD1=
,AD1= ,先求出△AD1C和△ACE的面积,再求出三棱锥D1-AEC的体积,由此能够求出点E到面ACD1的距离.进而得到体积。
,先求出△AD1C和△ACE的面积,再求出三棱锥D1-AEC的体积,由此能够求出点E到面ACD1的距离.进而得到体积。(1)证明:∵ ABCD-A1B1C1D1是长方体
∴AB// D1C1,AB=D1C1, ……1分
∴AB C1 D1为平行四边形,……2分
∴B C1 // AD1, ……3分
又B C1
 平面ACD1,AD1Ì平面ACD1, ……4分
平面ACD1,AD1Ì平面ACD1, ……4分所以BC1//平面ACD1. ……5分
(2) 证明:∵ AE⊥平面AA1D1D,A1DÌ平面AA1D1D,
∴ A1D⊥AE, ……6分
AA1D1D为正方形,∴A1D⊥A D1, ……7分
又A1D∩AE =A,∴A1D⊥平面AD1E, ……9分
A1DÌ平面AD1E,∴A1D⊥D1E, ……10分
(3) 解:
 , ……12分
, ……12分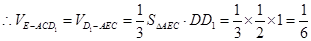 ……13分
……13分所以E-ACD1的体积为
 . ……14分
. ……14分点评:解决该试题的关键是对于线面平行的判定定理和线面垂直的性质定理的灵活运用和熟练掌握,同时对于体积的求解,一般就是研究几何体的高既可以得到。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目

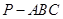 中,
中, 底面
底面 , 点
, 点 ,
, 分别在棱
分别在棱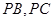 上,且
上,且

 平面
平面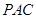 ;
; 的中点时,求
的中点时,求 与平面
与平面







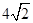








 内有一个球与正方体的各个面都相切,经过
内有一个球与正方体的各个面都相切,经过 和
和 作一个截面,正确的截面图是 .
作一个截面,正确的截面图是 .