题目内容
5.计算log5$\sqrt{\frac{6}{5}}$+log5$\sqrt{\frac{1}{6}}$+log4$\sqrt{8}$的值.分析 由对数的运算性质,有理数指数幂的运算性质,换底公式及其推论代入运算可得答案.
解答 解:log5$\sqrt{\frac{6}{5}}$+log5$\sqrt{\frac{1}{6}}$+log4$\sqrt{8}$=log5($\sqrt{\frac{6}{5}}$•$\sqrt{\frac{1}{6}}$)+log4$\sqrt{8}$=log5(${5}^{-\frac{1}{2}}$)+l0g22(${2}^{\frac{3}{2}}$)=$-\frac{1}{2}$+$\frac{3}{4}$=$\frac{1}{4}$
点评 本题考查的知识点是对数的运算性质,熟练掌握对数的运算性质,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.函数y=|x+1|+1的图象是( )
| A. | 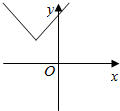 | B. | 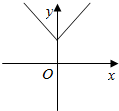 | C. | 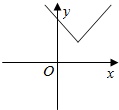 | D. | 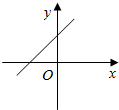 |
17.下列函数中,对于任意x∈R,同时满足条件f(x)=f(-x)和f(x-π)=f(x)的函数是( )
| A. | f(x)=sinx | B. | f(x)=sinx•cosx | C. | f(x)=cosx | D. | f(x)=cos2x-sin2x |