题目内容
15.设$f(x)=\left\{\begin{array}{l}1-cos\frac{πx}{2},x∈[0,1]\\ \frac{1}{x},x∈(1,e]\end{array}\right.$(其中e为自然对数的底数),则y=f(x)的图象与直线y=0,x=e所围成图形的面积为2-$\frac{2}{π}$.分析 分别作出f(x)的图象和直线x=e,由定积分知识可得,所求面积为${∫}_{0}^{1}(1-cos\frac{πx}{2})dx$+${∫}_{1}^{e}\frac{1}{x}dx$,计算即可得到.
解答 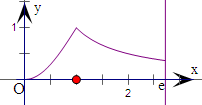 解:作出函数f(x)=$\left\{\begin{array}{l}{1-cos\frac{πx}{2},x∈[0,1]}\\{\frac{1}{x},x∈(1,e]}\end{array}\right.$的图象,
解:作出函数f(x)=$\left\{\begin{array}{l}{1-cos\frac{πx}{2},x∈[0,1]}\\{\frac{1}{x},x∈(1,e]}\end{array}\right.$的图象,
和直线x=e,如右图.
即有y=f(x)的图象与直线y=0,x=e所围成图形的面积
为${∫}_{0}^{1}(1-cos\frac{πx}{2})dx$+${∫}_{1}^{e}\frac{1}{x}dx$=(x-$\frac{2}{π}$sin$\frac{πx}{2}$)|${\;}_{0}^{1}$+lnx|${\;}_{1}^{e}$
=1-$\frac{2}{π}$sin$\frac{π}{2}$-0+lne-ln1=2-$\frac{2}{π}$.
故答案为:2-$\frac{2}{π}$.
点评 本题考查分段函数的运用,主要考查分段函数的图象和定积分的运用:求面积,考查运算能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
5. 某个四面体的三视图如图(其中三个正方形的边长均为1)所示,则该几何体的体积为( )
某个四面体的三视图如图(其中三个正方形的边长均为1)所示,则该几何体的体积为( )
 某个四面体的三视图如图(其中三个正方形的边长均为1)所示,则该几何体的体积为( )
某个四面体的三视图如图(其中三个正方形的边长均为1)所示,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
10.现有某工厂生产的甲、乙、丙、丁四种不同型号的产品分别有150件、120件、180件、150件.为了调查产品的情况,需从这600件产品中抽取一个容量为100的样本,若采用分层抽样,设甲产品中应抽取产品件数为x,设此次抽样中,某件产品A被抽到的概率为y,则x,y的值分别为( )
| A. | 25,$\frac{1}{4}$ | B. | 20,$\frac{1}{6}$ | C. | 25,$\frac{1}{600}$ | D. | 25,$\frac{1}{6}$ |
20.若复数z=1-i,i为虚数单位,则$\frac{2-z}{z}$=( )
| A. | -i | B. | i | C. | -1 | D. | 1 |
 已知函数f(x)=x2-ax的图象在点A(1,f(1))处的切线与直线x+3y+2=0垂直,执行如图所示的程序框图,输出的k值是6.
已知函数f(x)=x2-ax的图象在点A(1,f(1))处的切线与直线x+3y+2=0垂直,执行如图所示的程序框图,输出的k值是6.