题目内容
5.设Sn为等差数列{an}的前n项和.若a3+a8=3,S3=1,则通项公式an=$\frac{n-1}{3}$.分析 由题意可得首项和公差的方程组,解方程组可得首项和公差,可得通项公式.
解答 解:设等差数列{an}的公差为d,
∵a3+a8=3,S3=1,
∴a3+a8=2a1+9d=3,S3=3a1+3d=1,
解得a1=0,d=$\frac{1}{3}$,
∴通项公式an=0+$\frac{1}{3}$(n-1)=$\frac{n-1}{3}$
故答案为:$\frac{n-1}{3}$
点评 本题考查等差数列的通项公式和求和公式,属基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
20. 某商场每天上午10 点开门,晚上 19 点停止进入.在如图所示的框图中,t表示整点时刻,a(t )表示时间段[t-1,t)内进入商场人次,S 表示某天某整点时刻前进入商场人次总和,为了统计某天进入商场的总人次数,则判断框内可以填( )
某商场每天上午10 点开门,晚上 19 点停止进入.在如图所示的框图中,t表示整点时刻,a(t )表示时间段[t-1,t)内进入商场人次,S 表示某天某整点时刻前进入商场人次总和,为了统计某天进入商场的总人次数,则判断框内可以填( )
 某商场每天上午10 点开门,晚上 19 点停止进入.在如图所示的框图中,t表示整点时刻,a(t )表示时间段[t-1,t)内进入商场人次,S 表示某天某整点时刻前进入商场人次总和,为了统计某天进入商场的总人次数,则判断框内可以填( )
某商场每天上午10 点开门,晚上 19 点停止进入.在如图所示的框图中,t表示整点时刻,a(t )表示时间段[t-1,t)内进入商场人次,S 表示某天某整点时刻前进入商场人次总和,为了统计某天进入商场的总人次数,则判断框内可以填( )| A. | t≤17? | B. | t≥19? | C. | t≥18? | D. | t≤18? |
10.已知全集U={a,b,c,d},集合A={a,b},B={b,c},则∁U(A∪B)等于( )
| A. | {b} | B. | {d} | C. | {a,c,d} | D. | {a,b,c} |
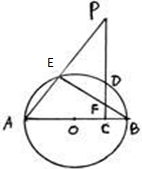 如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂足为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂足为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点