若复数z=1-i.i为虚数单位.则$\frac{2-z}{z}$=( )A．-iB．iC．-1D．1 题目和参考答案——青夏教育精英家教网—

题目内容

20．若复数z=1-i，i为虚数单位，则$\frac{2-z}{z}$=（　　）

A．

-i

B．

C．

-1

D．

分析利用复数的运算法则、共轭复数的定义即可得出．

解答解：$\frac{2-z}{z}$=$\frac{2-（1-i）}{1-i}$=$\frac{1+i}{1-i}$=$\frac{（1+i）^{2}}{（1-i）（1+i）}$=$\frac{2i}{2}$=i，
故选：B．

点评本题考查了复数的运算法则、共轭复数的定义，属于基础题．

练习册系列答案

11．已知S_n=-4n²+5n．求：
（1）a_n和a₂₁．
（2）{a_n}中满足-100＜a_n＜-20的所有各项的和．

8．若复数$z=\frac{1+i}{1-i}$，则$\overline z$的虚部为（　　）

15．设$f（x）=\left\{\begin{array}{l}1-cos\frac{πx}{2}，x∈[0，1]\\ \frac{1}{x}，x∈（1，e]\end{array}\right.$（其中e为自然对数的底数），则y=f（x）的图象与直线y=0，x=e所围成图形的面积为2-$\frac{2}{π}$．

5．在钝角△ABC中，若AB=2，$BC=\sqrt{2}$，且S_△ABC=1，则AC=（　　）

12．曲线$y=\frac{x^2}{lnx}$在点（e，e²）处的切线与直线x+ay=1垂直，则实数a的值为（　　）

9．

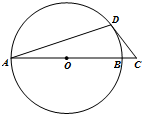如图，AB是圆O的直径，CD与圆O相切于点D，AB=8，BC=1，则CD=3；AD=$\frac{12\sqrt{10}}{5}$．

10．已知全集U={a，b，c，d}，集合A={a，b}，B={b，c}，则∁_U（A∪B）等于（　　）

试题分类