题目内容
已知函数f（x）=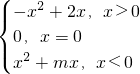
为奇函数，若函数f（x）在区间[-1，|a|-2]上单调递增，则a的取值范围是________．
[-3，-1）∪（1，3]
分析：根据函数是减函数，可得函数的单调递增区间，利用函数f（x）在区间[-1，|a|-2]上单调递增，建立不等式，即可求得a的取值范围．
解答：由题意，函数的单调递增区间为[-1，1]
∵函数f（x）在区间[-1，|a|-2]上单调递增，
∴-1＜|a|-2≤1，
∴1＜|a|≤3
∴a的取值范围是[-3，-1）∪（1，3]．
故答案为：[-3，-1）∪（1，3]
点评：本题考查函数单调性与奇偶性的结合，考查学生的计算能力，属于中档题．
分析：根据函数是减函数，可得函数的单调递增区间，利用函数f（x）在区间[-1，|a|-2]上单调递增，建立不等式，即可求得a的取值范围．
解答：由题意，函数的单调递增区间为[-1，1]
∵函数f（x）在区间[-1，|a|-2]上单调递增，
∴-1＜|a|-2≤1，
∴1＜|a|≤3
∴a的取值范围是[-3，-1）∪（1，3]．
故答案为：[-3，-1）∪（1，3]
点评：本题考查函数单调性与奇偶性的结合，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=
函数f（x）在哪点连续（ ）
|
| A、处处连续 | ||
| B、x=1 | ||
| C、x=0 | ||
D、x=
|