题目内容
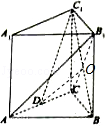
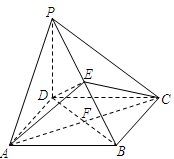
如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面ACC1A;
(3)求三棱锥C﹣BC1D的体积.
(1)证明见解析;(2)证明见解析;(3)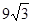 .
.
解析试题分析:
解题思路:(1)构造三角形的中位线,得出线线平行,再利用线面平行的判定定理进行证明;(2)利用线面垂直的性质及等边三角形的三线合一得出线线垂直,进而利用面面垂直的判定定理进行证明;(3)合理转化三棱锥的顶点求体积.
规律总结:证明空间中的线线、线面、面面的平行、垂直关系,关键合理选择性质定理或判定定理,进行三者之间的相互转化,线线关系是关键;求几何体的体积,要合理选择顶点与底面,以便容易求得高与面积.
试题解析:(1)证明:连接B1C交BC1于点O,连接OD,则点O为B1C的中点.
∵D为AC中点,得DO为△AB1C中位线,∴A1B∥OD.
∴直线AB1∥平面BC1D;
(2)证明:∵AA1⊥底面ABC,∴AA1⊥BD,
∵底面ABC正三角形,D是AC的中点
∴BD⊥AC
∵AA1∩AC=A,∴BD⊥平面ACC1A1,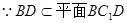 ,
,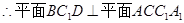 ;
;
(3)由(2)知,△ABC中,BD⊥AC,BD=BCsin60°=3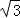 ,
,
∴S△BCD=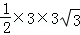 =
= ,
,
∴VC﹣BC1D=VC1﹣BCD=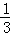 •
• •6=9
•6=9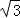 .
. 
考点:1.空间中的平行与垂直的判定;2.空间几何体的体积.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
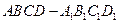 的各顶点都在球
的各顶点都在球 的球面上,其中
的球面上,其中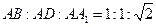 .
. 两点的球面距离记为
两点的球面距离记为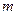 ,
,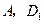 两点的球面距离记为
两点的球面距离记为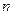 ,则
,则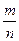 的值为 .
的值为 .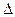 BCD的三条高线的交点;
BCD的三条高线的交点;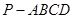 的底面
的底面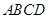 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中 ,
,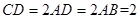 ,平面
,平面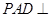 底面
底面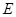 是
是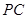 的中点.
的中点.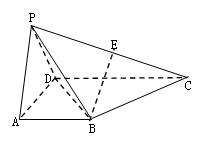
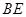 //平面
//平面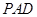 ;
;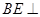
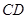 ;
; 的体积
的体积 .
.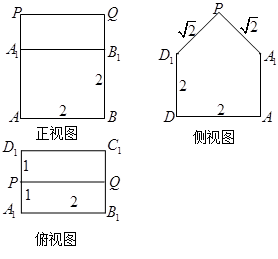
 的直观图及三视图如图所示,
的直观图及三视图如图所示,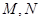 分别为
分别为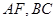 的中点.
的中点.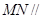 平面
平面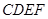 ;
;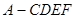 的体积.
的体积.
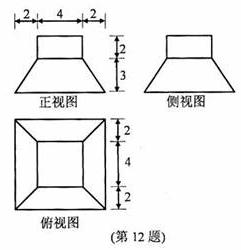
 .
.