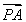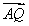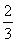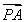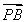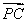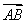题目内容
已知数列{an}满足a1=a(a>0,a∈N*),a1+a2+…+an-pan+1=0(p≠0,p≠-1,n∈N*).
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
(1)an= (2)①p=-
(2)①p=-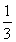 ,dk=9a·2k-1或p=-
,dk=9a·2k-1或p=-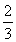 ,dk=
,dk=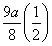 k-1②a=13.
k-1②a=13.
【解析】(1)因为a1+a2+…+an-pan+1=0,所以n≥2时,a1+a2+…+an-1-pan=0,两式相减,得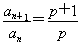 (n≥2),故数列{an}从第二项起是公比为
(n≥2),故数列{an}从第二项起是公比为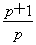 的等比数列,又当n=1时,a1-pa2=0,解得a2=
的等比数列,又当n=1时,a1-pa2=0,解得a2=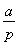 ,
,
从而an=
(2)①由(1)得ak+1=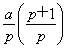 k-1,ak+2=
k-1,ak+2=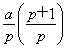 k,ak+3=
k,ak+3=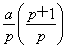 k+1,
k+1,
若ak+1为等差中项,则2ak+1=ak+2+ak+3,
即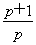 =1或
=1或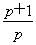 =-2,解得p=-
=-2,解得p=-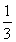 ;
;
此时ak+1=-3a(-2)k-1,ak+2=-3a(-2)k,
所以dk=|ak+1-ak+2|=9a·2k-1,
若ak+2为等差中项,则2ak+2=ak+1+ak+3,即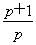 =1,此时无解;
=1,此时无解;
若ak+3为等差中项,则2ak+3=ak+1+ak+2,即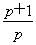 =1或
=1或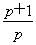 =-
=-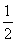 ,
,
解得p=-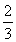 ,
,
此时ak+1=-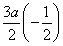 k-1,ak+3=-
k-1,ak+3=-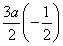 k+1,所以dk=|ak+1-ak+3|=
k+1,所以dk=|ak+1-ak+3|=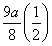 k-1,
k-1,
综上所述,p=-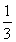 ,dk=9a·2k-1或p=-
,dk=9a·2k-1或p=-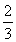 ,dk=
,dk=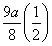 k-1.
k-1.
②当p=-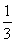 时,Sk=9a(2k-1).
时,Sk=9a(2k-1).
则由Sk<30,得a<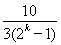 ,
,
当k≥3时,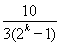 <1,所以必定有a<1,
<1,所以必定有a<1,
所以不存在这样的最大正整数.
当p=-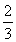 时,Sk=
时,Sk=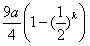 ,
,
则由Sk<30,得a< ,因为
,因为 >
>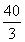 ,所以a=13满足Sk<30恒成立;但当a=14时,存在k=5,使得a>
,所以a=13满足Sk<30恒成立;但当a=14时,存在k=5,使得a> 即Sk<30,
即Sk<30,
所以此时满足题意的最大正整数a=13

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案