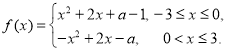题目内容
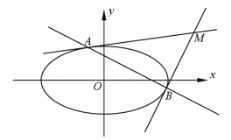
【题目】已知动点![]() 满足
满足![]() ,记M的轨迹为曲线C,直线l:
,记M的轨迹为曲线C,直线l:![]() (
(![]() )交曲线C于P,Q两点,点P在第一象限,
)交曲线C于P,Q两点,点P在第一象限,![]() 轴,垂足为E,连接QE并延长交曲线C于点G.
轴,垂足为E,连接QE并延长交曲线C于点G.
(1)求曲线C的方程,并说明曲线C是什么曲线;
(2)若![]() ,求
,求![]() 的面积.
的面积.
(3)求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,轨迹是以
,轨迹是以![]() 、
、![]() 为焦点的椭圆
为焦点的椭圆
(2)![]()
(3)![]()
【解析】
(1)根据![]() ,由两点间的距离公式可看出,其表示动点
,由两点间的距离公式可看出,其表示动点![]() 与两定点
与两定点![]() 、
、![]() 的距离之和为
的距离之和为![]() ,且
,且![]() ,可知其符合椭圆的定义,把相关量代入椭圆标准方程,即可求解;
,可知其符合椭圆的定义,把相关量代入椭圆标准方程,即可求解;
(2)写出直线![]() 的方程与曲线
的方程与曲线![]() 的方程联立,便可解出点
的方程联立,便可解出点![]() 坐标,进而知道点
坐标,进而知道点![]() 的坐标,再求出直线
的坐标,再求出直线![]() 的方程后,与曲线
的方程后,与曲线![]() 的方程联立,可解出点
的方程联立,可解出点![]() 的坐标,再代
的坐标,再代![]() 公式,即可求出面积;
公式,即可求出面积;
(3)将直线![]() 的方程与曲线
的方程与曲线![]() 的方程联立,解出点
的方程联立,解出点![]() 坐标,进而得点
坐标,进而得点![]() 的坐标,再求出直线
的坐标,再求出直线![]() 的方程后,与曲线
的方程后,与曲线![]() 的方程联立,可得点
的方程联立,可得点![]() 坐标,再根据点
坐标,再根据点![]() 坐标,得直线
坐标,得直线![]() 的斜率,可验证
的斜率,可验证![]() ,得
,得![]() 是直角三角形,代两点间的距离公式可求出
是直角三角形,代两点间的距离公式可求出![]() ,所以
,所以![]() 是一个关于直线
是一个关于直线![]() 的斜率的函数,由函数求最值的方法,即可求解.
的斜率的函数,由函数求最值的方法,即可求解.
(1)由![]() ,可得点
,可得点![]() 到点
到点![]() 、
、![]() 的距离之和为4且
的距离之和为4且![]() ,所以动点
,所以动点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 的椭圆,其中
的椭圆,其中![]() ,
,![]() ,即
,即![]() ,
,![]() ,所以曲线C的轨迹方程为
,所以曲线C的轨迹方程为![]() ,轨迹是以
,轨迹是以![]() 、
、![]() 的椭圆.
的椭圆.
(2)根据题![]() 意得,与
意得,与![]() 联立
联立
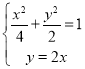 ,解得
,解得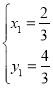 或
或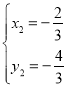
所以P点坐标为![]() ,Q点坐标为
,Q点坐标为![]()
因为![]() 轴,垂足为E,所以E点坐标为
轴,垂足为E,所以E点坐标为![]()
所以直线QE方程为![]()
与![]() 联立,可得
联立,可得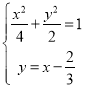 ,整理可得
,整理可得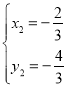 或
或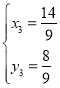
所以G点坐标为![]()
![]()
(3)设直线PQ的斜率为k,则其方程为![]() (
(![]() ).由
).由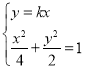 得
得![]() .
.
记![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
于是直线QG的斜率为![]() ,方程为
,方程为![]() .
.
由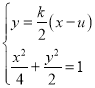 得
得![]() ——①
——①
设![]() ,则
,则![]() 和
和![]() 是方程①的解,故
是方程①的解,故![]() .由此得
.由此得![]() .
.
从而直线PG的斜率为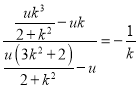 .
.
所以![]() ,即
,即![]() 是直角三角形.
是直角三角形.
得![]() ,
,![]() .
.
所以![]() 的面积
的面积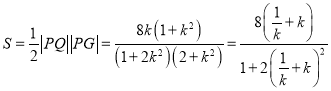 .
.
设![]() ,则由
,则由![]() 得
得![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
因为![]() 在
在![]() 单调递减,所以当
单调递减,所以当![]() ,即
,即![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.
因此,![]() 面积的最大值为
面积的最大值为![]() .
.

 字词句段篇系列答案
字词句段篇系列答案【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: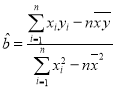 ,
,![]() ,
,![]() ,
,![]() .
.