题目内容
11.已知函数f(x)=x|x+m|-4,m∈R(1)若g(x)=f(x)+4为奇函数,求实数m的值;
(2)当m=-3时,求函数f(x)在x∈[3,4]上的值域;
(3)若f(x)<0对x∈(0,1]恒成立,求实数m的取值范围.
分析 (1)化简g(x)=f(x)+4=x|x+m|,从而可得-x|-x+m|=-x|x+m|,化简可得mx=0对x∈R恒成立,从而解得;
(2)当m=-3时,化简f(x)=x(x-3)-4=x2-3x-4在[3,4]上为增函数,从而求函数的值域;
(3)化简可得x|x+m|-4<0,从而可得$-\frac{4}{x}<x+m<\frac{4}{x}$,令$h(x)=-(x+\frac{4}{x})$,则h(x)在(0,1]上是增函数,再令$t(x)=\frac{4}{x}-x$,则t(x)在(0,1]上是减函数,从而求最值,从而解得.
解答 解:(1)g(x)=f(x)+4=x|x+m|,
∵函数g(x)为奇函数,∴g(-x)=-g(x)
∴-x|-x+m|=-x|x+m|,
即x(|x+m|-|x-m|)=0对x∈R恒成立,
∴|x+m|-|x-m|=0对x∈R恒成立,
即(x+m)2=(x-m)2对x∈R恒成立,
即mx=0对x∈R恒成立,
∴m=0;
(2)当m=-3时,
∵x∈[3,4],
∴f(x)=x(x-3)-4=x2-3x-4,
∵f(x)在[3,4]上为增函数,
∴y∈[-4,0];
(3)f(x)<0即为x|x+m|-4<0,
∵x∈(0,1],∴$|x+m|<\frac{4}{x}$,
即$-\frac{4}{x}<x+m<\frac{4}{x}$,
即$-(x+\frac{4}{x})<m<\frac{4}{x}-x$对x∈(0,1]恒成立,
令$h(x)=-(x+\frac{4}{x})$,则h(x)在(0,1]上是增函数,
∴h(x)max=h(1)=-5,
∴m>-5;
再令$t(x)=\frac{4}{x}-x$,则t(x)在(0,1]上是减函数,
∴t(x)min=t(1)=3,
∴m<3,
综上,实数m的取值范围是-5<m<3.
点评 本题考查了函数的性质的判断与应用,同时考查了恒成立问题及最值问题.

| A. | 直线θ=$\frac{π}{3}$对称 | B. | 直线θ=$\frac{5π}{6}$对称 | C. | 点$(2,\frac{π}{3})$对称 | D. | 极点对称 |
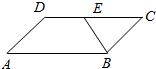 如图,在平行四边形ABCD中,E是CD中点,$\overrightarrow{BE}=x\overrightarrow{AB}+y\overrightarrow{AD}$,则x+y=$\frac{1}{2}$.
如图,在平行四边形ABCD中,E是CD中点,$\overrightarrow{BE}=x\overrightarrow{AB}+y\overrightarrow{AD}$,则x+y=$\frac{1}{2}$.