题目内容
5.已知数列{an}是各项均为正数的等比数列,满足a3=8,a3-a2-2a1=0.(Ⅰ)求数列{an}的通项公式
(Ⅱ)记bn=log2an,求数列{an•bn}的前n项和Sn.
分析 (Ⅰ)设数列{an}的公比为q,通过a3-a2-2a1=0,可得q=2,利用a3=8可得a1=2,进而可得结论;
(Ⅱ)通过bn=$lo{g}_{2}{2}^{n}$=n,可得anbn=n•2n,分别写出Sn、与2Sn的表达式,利用错位相减法及等比数列的求和公式即得结论.
解答 解:(Ⅰ)设数列{an}的公比为q,
由an>0可得q>0,且a3-a2-2a1=0,
化简得q2-q-2=0,
解得q=2或q=-1(舍),
∵a3=a1•q2=4a1=8,∴a1=2,
∴数列{an}是以首项和公比均为2的等比数列,
∴an=2n;
(Ⅱ)由(I)知bn=log2an=$lo{g}_{2}{2}^{n}$=n,
∴anbn=n•2n,
∴Sn=1×21+2×22+3×23+…+(n-1)×2n-1+n×2n,
2Sn=1×22+2×23+…+(n-2)×2n-1+(n-1)×2n+n×2n+1,
两式相减,得-Sn=21+22+23+…+2n-1+2n-n×2n+1,
∴-Sn=$\frac{2(1-{2}^{n})}{1-2}$-n×2n+1,
∴Sn=2+(n-1)2n+1.
点评 本题考查等比数列的通项公式,错位相减法求和等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查函数与方程思想、化归与转化思想,注意解题方法的积累,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
15.执行如图的程序框图,若输入x=7,y=6,则输出的有序数对为( )
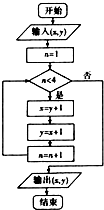

| A. | (9,10) | B. | (12,13) | C. | (13,14) | D. | (13,12) |
13.“a=2”是“直线x+y=0与直线2x-ay=0互相垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)求x的值并估计全校3000名学生中读书谜大概有多少?(经频率视为频率)
(2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$n=a+b+c+d

(1)求x的值并估计全校3000名学生中读书谜大概有多少?(经频率视为频率)
| 非读书迷 | 读书迷 | 合计 | |
| 男 | 15 | ||
| 女 | 45 | ||
| 合计 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$n=a+b+c+d
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
