题目内容
已知椭圆 (a>b>0)的中心为O,左焦点为F,A是椭圆上的一点,
(a>b>0)的中心为O,左焦点为F,A是椭圆上的一点, 且
且 ,则该椭圆的离心率是
,则该椭圆的离心率是
- A.
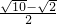
- B.
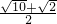
- C.
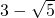
- D.
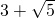
A
分析:通过向量的数量积判断三角形是等腰直角三角形,求出A的坐标,代入椭圆方程然后求出椭圆的离心率.
解答:因为已知椭圆 (a>b>0)的中心为O,左焦点为F,A是椭圆上的一点,
(a>b>0)的中心为O,左焦点为F,A是椭圆上的一点,
因为 ,所以
,所以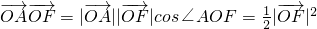 ,又
,又 ,
,
所以 ,所以cos∠AOF=
,所以cos∠AOF= ,所以三角形AOF是等腰直角三角形,
,所以三角形AOF是等腰直角三角形,
A(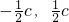 ),代入椭圆方程可得:
),代入椭圆方程可得: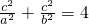 ,又b2=a2-c2,
,又b2=a2-c2,
可得:e4-6e2+4=0
解得e=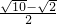 .
.
故选A.
点评:本题考查椭圆的简单性质的应用,向量的数量积的应用,考查计算能力.
分析:通过向量的数量积判断三角形是等腰直角三角形,求出A的坐标,代入椭圆方程然后求出椭圆的离心率.
解答:因为已知椭圆
 (a>b>0)的中心为O,左焦点为F,A是椭圆上的一点,
(a>b>0)的中心为O,左焦点为F,A是椭圆上的一点,因为
 ,所以
,所以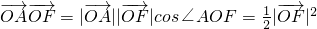 ,又
,又 ,
,所以
 ,所以cos∠AOF=
,所以cos∠AOF= ,所以三角形AOF是等腰直角三角形,
,所以三角形AOF是等腰直角三角形,A(
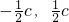 ),代入椭圆方程可得:
),代入椭圆方程可得: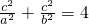 ,又b2=a2-c2,
,又b2=a2-c2,可得:e4-6e2+4=0
解得e=
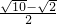 .
.故选A.
点评:本题考查椭圆的简单性质的应用,向量的数量积的应用,考查计算能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.