题目内容
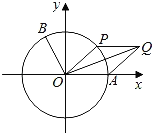
【题目】如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为(2-p , -p);
②求p的取值范围.
【答案】
(1)
解: ![]() ,
, ![]()
![]() 与
与 ![]() 轴的交点坐标为
轴的交点坐标为 ![]()
即抛物线的焦点为 ![]() ,
, ![]()
![]()
(2)
解:① 设点 ![]() ,
, ![]()
则: ![]() ,即
,即 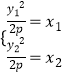 ,
, 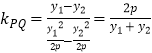
又 ![]() 关于直线
关于直线 ![]() 对称,
对称, ![]()
即 ![]() ,
, ![]()
又 ![]() 中点一定在直线
中点一定在直线 ![]() 上
上
![]()
![]() 线段
线段 ![]() 上的中点坐标为
上的中点坐标为 ![]() ;
;
② ![]() 中点坐标为
中点坐标为 ![]()
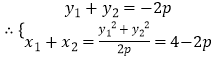 即
即 ![]()
![]() ,即关于
,即关于 ![]() 有两个不等根
有两个不等根
![]() ,
, ![]() ,
, ![]()
【解析】(1)求出抛物线的焦点坐标,然后求解抛物线方程.(2):①设点P(x1 , y1),Q(x2 , y2),通过抛物线方程,求解kPQ , 通过P,Q关于直线l对称,点的kPQ=﹣1,推出 ![]() ,PQ的中点在直线l上,推出
,PQ的中点在直线l上,推出 ![]() =2﹣p,即可证明线段PQ的中点坐标为(2﹣p,﹣p);②利用线段PQ中点坐标(2﹣p,﹣p).推出
=2﹣p,即可证明线段PQ的中点坐标为(2﹣p,﹣p);②利用线段PQ中点坐标(2﹣p,﹣p).推出 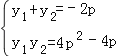 ,得到关于y2+2py+4p2﹣4p=0,有两个不相等的实数根,列出不等式即可求出p的范围.
,得到关于y2+2py+4p2﹣4p=0,有两个不相等的实数根,列出不等式即可求出p的范围.

练习册系列答案
相关题目