题目内容
 如图,已知椭圆
如图,已知椭圆 =1(a>b>0),F1、F2分别为椭
=1(a>b>0),F1、F2分别为椭
圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一
点B、
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若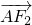 =2
=2 ,
, •
• =
= ,求椭圆的方程.
,求椭圆的方程.
解:(1)若∠F1AB=90°,则△AOF2为等腰直角三角形,所以有OA=OF2,即b=C、
所以a= c,e=
c,e= =
= .
.
(2)由题知A(0,b),F1(-c,0),F2(c,0),
其中,c= ,设B(x,y).
,设B(x,y).
由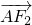 =2
=2 ?(c,-b)=2(x-c,y),解得x=
?(c,-b)=2(x-c,y),解得x=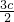 ,
,
y=- ,即B(
,即B(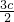 ,-
,- ).
).
将B点坐标代入 =1,得
=1,得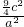 +
+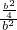 =1,
=1,
即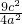 +
+ =1,
=1,
解得a2=3c2.①
又由 •
• =(-c,-b)•(
=(-c,-b)•(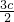 ,-
,-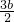 )=
)=
?b2-c2=1,
即有a2-2c2=1.②
由①,②解得c2=1,a2=3,从而有b2=2.
所以椭圆方程为 +
+ =1.
=1.
分析:(1)根据∠F1AB=90°推断出△AOF2为等腰直角三角形,进而可知OA=OF2,求得b和c的关系,进而可求得a和c的关系,即椭圆的离心率.
(2)根据题意可推断出A,和两个焦点的坐标,设出B的坐标,利用已知条件中向量的关系,求得x和y关于c的表达式,代入椭圆方程求得a和c的关系,利用 •
• =
= 求得a和c的关系,最后联立求得a和b,则椭圆方程可得.
求得a和c的关系,最后联立求得a和b,则椭圆方程可得.
点评:本题主要考查了椭圆的应用和椭圆的简单性质,向量的基本性质.注意挖掘题意中隐含的条件,充分利用.
所以a=
 c,e=
c,e= =
= .
.(2)由题知A(0,b),F1(-c,0),F2(c,0),
其中,c=
 ,设B(x,y).
,设B(x,y).由
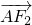 =2
=2 ?(c,-b)=2(x-c,y),解得x=
?(c,-b)=2(x-c,y),解得x=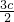 ,
,y=-
 ,即B(
,即B(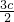 ,-
,- ).
).将B点坐标代入
 =1,得
=1,得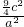 +
+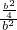 =1,
=1,即
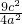 +
+ =1,
=1,解得a2=3c2.①
又由
 •
• =(-c,-b)•(
=(-c,-b)•(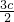 ,-
,-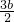 )=
)=
?b2-c2=1,
即有a2-2c2=1.②
由①,②解得c2=1,a2=3,从而有b2=2.
所以椭圆方程为
 +
+ =1.
=1.分析:(1)根据∠F1AB=90°推断出△AOF2为等腰直角三角形,进而可知OA=OF2,求得b和c的关系,进而可求得a和c的关系,即椭圆的离心率.
(2)根据题意可推断出A,和两个焦点的坐标,设出B的坐标,利用已知条件中向量的关系,求得x和y关于c的表达式,代入椭圆方程求得a和c的关系,利用
 •
• =
= 求得a和c的关系,最后联立求得a和b,则椭圆方程可得.
求得a和c的关系,最后联立求得a和b,则椭圆方程可得.点评:本题主要考查了椭圆的应用和椭圆的简单性质,向量的基本性质.注意挖掘题意中隐含的条件,充分利用.

练习册系列答案
相关题目
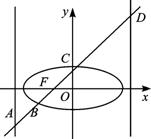
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
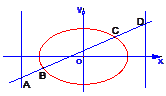
,求椭圆的方程.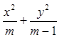 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线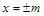 的交点从左到右的顺序为A、B、C、D,设
的交点从左到右的顺序为A、B、C、D,设 .
.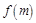 的解析式;
的解析式;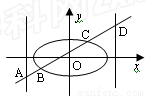
 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),离心率为
),离心率为 =2;
=2;