题目内容
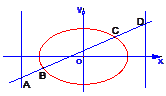
如图,已知椭圆![]() =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||
(1)求f(m)的解析式;
(2)求f(m)的最值.
(1) f(m)=![]() , m∈[2,5] (2) f(m)的最大值为
, m∈[2,5] (2) f(m)的最大值为![]() ,此时m=2;f(m)的最小值为
,此时m=2;f(m)的最小值为![]() ,此时m=5
,此时m=5
解析:
(1)设椭圆的半长轴、半短轴及半焦距依次为a、b、c,则a2=m,b2=m-1,c2=a2-b2=1
∴椭圆的焦点为F1(-1,0),F2(1,0).
故直线的方程为y=x+1,又椭圆的准线方程为x=±![]() ,即x=±m.
,即x=±m.
∴A(-m,-m+1),D(m,m+1)
考虑方程组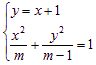 ,消去y得:(m-1)x2+m(x+1)2=m(m-1)
,消去y得:(m-1)x2+m(x+1)2=m(m-1)
整理得:(2m-1)x2+2mx+2m-m2=0
Δ=4m2-4(2m-1)(2m-m2)=8m(m-1)2
∵2≤m≤5,∴Δ>0恒成立,xB+xC=![]() .
.
又∵A、B、C、D都在直线y=x+1上
∴|AB|=|xB-xA|=![]() =(xB-xA)·
=(xB-xA)·![]() ,|CD|=
,|CD|=![]() (xD-xC)
(xD-xC)
∴||AB|-|CD||=![]() |xB-xA+xD-xC|=
|xB-xA+xD-xC|=![]() |(xB+xC)-(xA+xD)|
|(xB+xC)-(xA+xD)|
又∵xA=-m,xD=m,∴xA+xD=0
∴||AB|-|CD||=|xB+xC|·![]() =|
=|![]() |·
|·![]() =
=![]() (2≤m≤5)
(2≤m≤5)
故f(m)=![]() ,m∈[2,5].
,m∈[2,5].
(2)由f(m)=![]() ,可知f(m)=
,可知f(m)=![]()
又2-![]() ≤2-
≤2-![]() ≤2-
≤2-![]() ,∴f(m)∈[
,∴f(m)∈[![]() ]
]
故f(m)的最大值为![]() ,此时m=2;f(m)的最小值为
,此时m=2;f(m)的最小值为![]() ,此时m=5.
,此时m=5.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
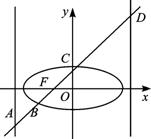
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程.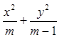 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线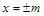 的交点从左到右的顺序为A、B、C、D,设
的交点从左到右的顺序为A、B、C、D,设 .
.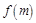 的解析式;
的解析式;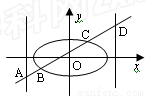
 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),离心率为
),离心率为 =2;
=2;