题目内容
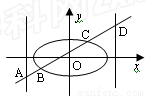
(12分)如图,已知椭圆 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),离心率为
),离心率为 ,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
(1)求椭圆的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2, 证明: =2;
=2;
【答案】
略
【解析】(1)因为椭圆过点(1,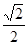 ),e=
),e=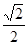 . 所以
. 所以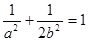 ,
,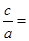
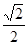 .
.
又a2=b2+c2,
所以a=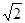 ,b=1, c=1.
,b=1, c=1.
(2)(i)证明:方法一:由于F1(-1,0)、F2(1,0),PF1、PF2的斜率分别为k1、k2,且点P不在x轴上.
所以k1≠k2,k1≠0,k2≠0.
又直线PF1,PF2的方程分别为y=k1(x+1),y=k2(x-1),
联立方程解得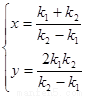
所以P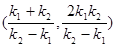 .
.
因此2k1k2+3k1-k2=0,即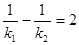 ,结论成立.
,结论成立.
方法二:设P(x0,y0),
则k1=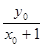 , k2=
, k2=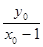 ,
,
因为点P不在x轴上,所以y0≠0.
又x0+y0=2,
所以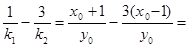

练习册系列答案
相关题目
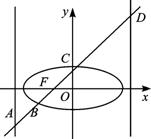
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
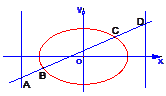
,求椭圆的方程.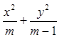 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线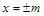 的交点从左到右的顺序为A、B、C、D,设
的交点从左到右的顺序为A、B、C、D,设 .
.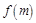 的解析式;
的解析式;