题目内容
【题目】如图1,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕将
为折痕将![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意可证得![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() 可证;
可证;
(2)解法一:利用等体积法由![]() 可求出点
可求出点![]() 到平面
到平面![]() 的距离;解法二:由条件知点
的距离;解法二:由条件知点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,过点
的距离,过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,证明
,证明![]() 平面
平面![]() ,计算出
,计算出![]() 即可.
即可.
解法一:(1)依题意知,因为![]() ,所以
,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .
.
由已知,![]() 是等边三角形,且
是等边三角形,且![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.


(2)在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
由(1)知,![]() 平面
平面![]() ,且
,且![]() ,
,
所以三棱锥![]() 的体积
的体积![]() .
.
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() ,
,
由(1)知,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,
,
设点![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
则三棱锥![]() 的体积
的体积![]() ,得
,得![]() .
.
解法二:(1)同解法一;
(2)因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,即
,即![]() .
.
由(1)知,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
由(1)知,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】为了解广大学生家长对校园食品安全的认识,某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查,每一位学生家长仅有一次参加机会,现对有效问卷进行整理,并随机抽取出了200份答卷,统计这些答卷的得分(满分:100分)制出的频率分布直方图如图所示,由频率分布直方图可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
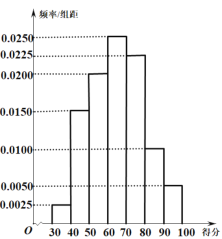
(1)请利用正态分布的知识求![]() ;
;
(2)该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费:
的可以获赠1次随机话费:
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) |
|
|
概率 |
|
|
市食品安全检测部门预计参加此次活动的家长约5000人,请依据以上数据估计此次活动可能赠送出多少话费?
附:①![]() ;②若
;②若![]() ;则
;则![]() ,
,![]() ,
,![]() .
.
【题目】下表是![]() 年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
时间(年) |
|
|
|
|
|
|
|
就业人口(万人) |
|
|
|
|
|
|
|
劳动年龄人口(万人) |
|
|
|
|
|
|
|
则由表可知( )
A.![]() 年我国就业人口逐年减少
年我国就业人口逐年减少
B.![]() 年我国劳动年龄人口逐年增加
年我国劳动年龄人口逐年增加
C.![]() 年这
年这![]() 年我国就业人口数量的中位数为
年我国就业人口数量的中位数为![]()
D.![]() 年我国劳动年龄人口中就业人口所占比重逐年增加
年我国劳动年龄人口中就业人口所占比重逐年增加