题目内容
设集合M={1,2,3,4,5,6},S1、S2、…、Sk都是M的含两个元素的子集,且满足:对任意的Si={ai,bi},Sj={aj,bj}(i≠j,i、j∈{1,2,3,…,k}),都有min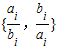 ≠min
≠min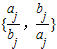 (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( )A.10
B.11
C.12
D.13
【答案】分析:根据题意,首先分析出M的所有含2个元素的子集数目,进而对其特殊的子集分析排除,注意对min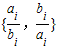 ≠min
≠min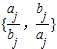 (min{x,y}表示两个数x、y中的较小者)的把握,即可得答案.
(min{x,y}表示两个数x、y中的较小者)的把握,即可得答案.
解答:解:根据题意,对于M,含2个元素的子集有15个,
但{1,2}、{2,4}、{3,6}只能取一个;
{1,3}、{2,6}只能取一个;
{2,3}、{4,6}只能取一个,
故满足条件的两个元素的集合有11个;
故选B.
点评:本题考查学生对集合及其子集、元素的把握、运用,注意对题意的分析.
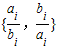 ≠min
≠min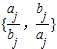 (min{x,y}表示两个数x、y中的较小者)的把握,即可得答案.
(min{x,y}表示两个数x、y中的较小者)的把握,即可得答案.解答:解:根据题意,对于M,含2个元素的子集有15个,
但{1,2}、{2,4}、{3,6}只能取一个;
{1,3}、{2,6}只能取一个;
{2,3}、{4,6}只能取一个,
故满足条件的两个元素的集合有11个;
故选B.
点评:本题考查学生对集合及其子集、元素的把握、运用,注意对题意的分析.

练习册系列答案
相关题目
设集合M={1,2},N={a2},则a=1是N?M的( )条件.
| A、充分不必要 | B、必要不充分 | C、充要 | D、既不充分也不必要 |
设集合M={1,2,3},N={1},则下列关系正确的是( )
| A、N∈M | B、N∉M | C、N=M | D、N?M |