题目内容
设直线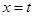 与函数
与函数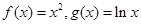 的图象分别交于点
的图象分别交于点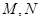 ,则当
,则当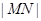 达到最小时
达到最小时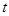 的值为( )
的值为( )
| A.1 | B.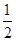 | C.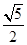 | D.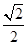 |
D.
解析试题分析:设直线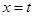 与两函数的交点为
与两函数的交点为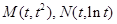 ,(其中
,(其中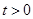 )则
)则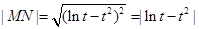 ,令
,令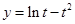 ,由
,由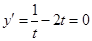 得,
得,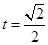 ,可以验证,当
,可以验证,当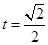 时,
时,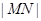 最小,选D.
最小,选D.
考点:1.两点间的距离公式;2.利用导数研究函数最值.

练习册系列答案
相关题目
已知函数 的导数为
的导数为 ,且满足关系式
,且满足关系式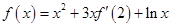 则
则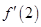 的值等于( )
的值等于( )
A.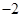 | B.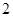 | C.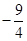 | D.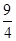 |
已知函数 有且仅有两个不同的零点
有且仅有两个不同的零点 ,
, ,则( )
,则( )
A.当 时, 时, , , |
B.当 时, 时, , , |
C.当 时, 时, , , |
D.当 时, 时, , , |
已知函数f(x)=x3+2bx2+cx+1有两个极值点x1、x2,且x1∈[-2,-1],x2∈[1,2],则f(-1)的取值范围是 ( )
| A.[-,3] | B.[,6] | C.[3,12] | D.[-,12] |
设函数 ,的导函数为
,的导函数为 ,且
,且 ,
, ,则下列不等式成立的是(注:e为自然对数的底数)( )
,则下列不等式成立的是(注:e为自然对数的底数)( )
A. | B. |
C. | D. |
已知定义域为R的奇函数f(x)的导函数为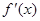 ,当
,当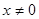 时,
时,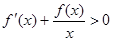 ,若
,若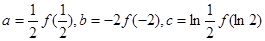 ,则下列关于a,b,c的大小关系正确的是( )
,则下列关于a,b,c的大小关系正确的是( )
| A.a>b>c | B.a>c>b | C.c>b>a | D.b>a>c |
已知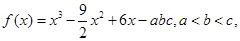 且
且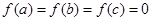 ,现给出如下结论:
,现给出如下结论:
①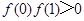 ;②
;②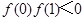 ;③
;③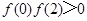 ;④
;④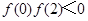 .其中正确结论的序号为:( )
.其中正确结论的序号为:( )
| A.①③ | B.①④ | C.②④ | D.②③ |
若实数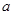 、
、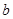 、
、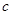 、
、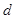 满足
满足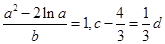 ,则
,则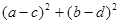 的最小值 为 ( )
的最小值 为 ( )
A.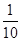 | B.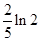 | C.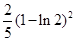 | D.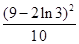 |
 的函数的导数,我们常采用以下做法:先两边同取自然对数得:
的函数的导数,我们常采用以下做法:先两边同取自然对数得: ,再两边同时求导得
,再两边同时求导得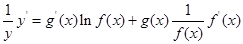 ,于是得到:
,于是得到: ,运用此方法求得函数
,运用此方法求得函数 的一个单调递增区间是( )
的一个单调递增区间是( )


