题目内容
若实数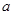 、
、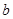 、
、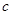 、
、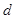 满足
满足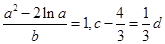 ,则
,则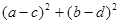 的最小值 为 ( )
的最小值 为 ( )
A.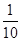 | B.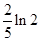 | C.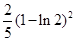 | D.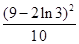 |
C
解析试题分析:因为,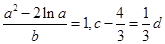 ,所以有点p(a,b)在函数
,所以有点p(a,b)在函数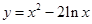 的图象上,点Q(c,d)在
的图象上,点Q(c,d)在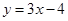 的图象上,
的图象上,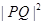 =
=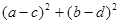 。即求曲线上的点到直线
。即求曲线上的点到直线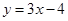 的距离平方的最小值,即求平行于
的距离平方的最小值,即求平行于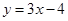 的切线的切点到直线距离平方。
的切线的切点到直线距离平方。
因为,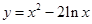 ,所以,
,所以, ,设切点为(m,n)(m>0),则
,设切点为(m,n)(m>0),则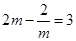 ,解得,m=2,n=4-2ln2,切点为(2,4-2ln2),故
,解得,m=2,n=4-2ln2,切点为(2,4-2ln2),故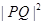 的最小值为
的最小值为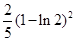 ,选B。
,选B。
考点:导数的几何意义,直线方程,点到直线的距离。
点评:中档题,本题综合性较强,利用转化与化归思想,应用导数使问题得到解决,较难想到。

练习册系列答案
相关题目
设直线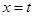 与函数
与函数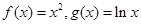 的图象分别交于点
的图象分别交于点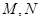 ,则当
,则当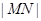 达到最小时
达到最小时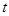 的值为( )
的值为( )
| A.1 | B.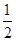 | C.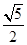 | D.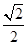 |
设曲线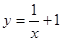 在点(1,2)处的切线与直线
在点(1,2)处的切线与直线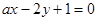 平行,则
平行,则 =( )
=( )
| A.-1 | B.0 | C.-2 | D.2 |
若曲线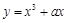 在坐标原点处的切线方程是
在坐标原点处的切线方程是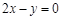 ,则实数
,则实数 ( )
( )
| A.1 | B.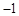 | C.2 | D.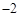 |
已知函数f(x)=2-|x|,则 =
=
| A.3 | B.4 | C.3.5 | D.4.5 |
对于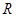 上可导的任意函数
上可导的任意函数 ,若满足
,若满足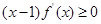 ,则必有( )
,则必有( )
A.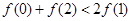 | B.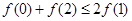 |
C.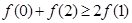 | D.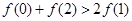 |
设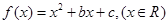 ,且满足
,且满足 ,对任意正实数
,对任意正实数 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )
A.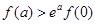 | B.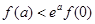 |
C.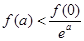 | D.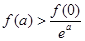 |
 满足:①当
满足:①当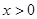 时,
时, 恒成立;②对任意的
恒成立;②对任意的 都有
都有 。又函数
。又函数 满足:对任意的
满足:对任意的 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式 对
对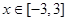 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )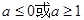

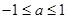
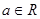
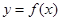 的导函数在区间
的导函数在区间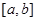 上是增函数,则函数
上是增函数,则函数